��Ŀ����
9���Ķ�����ͼ1����ֱ�ǡ�ABC�У���C=90�㣬AC��BCΪֱ�DZߣ�ABΪб�ߣ���BC=a��AC=b��AB=c����a2+b2=c2���磬AC=8��BC=6����ɵ�AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10
�����Ķ����ϣ������Ŀ��
��ͼ2��һ��ֱ�������ε��̵أ���������ֱ�DZ߳��ֱ�Ϊ6cm��8cm������Ҫ���̵�����ɵ��������Σ������䲿������8mΪֱ�DZߵ�ֱ�������Σ������������������̵ص��ܳ���

���� ������ĿҪ�������ACΪֱ�DZߵĵ���ֱ�������Σ���AC=BC����C=90�㣬Ȼ���ɹ��ɶ������AB�ij��������������ĵ���ֱ�������ε��ܳ����ɣ�
��� �⣺����ͼ1���ӳ�BC��D��ʹAB=AD������AD����AB=AD=10ʱ������CD=CB=6�á�ABD���ܳ�Ϊ32m��
����ͼ2����AB=BD=10ʱ������CD=4��
�ɹ��ɶ����ã�AD=4$\sqrt{5}$�á�ABD���ܳ�Ϊ��20+4$\sqrt{5}$��m��
����ͼ3����ABΪ��ʱ����AD=BD=x����CD=x-6���ɹ��ɶ����ã�x=$\frac{25}{3}$��
�á�ABD���ܳ�Ϊ$\frac{80}{3}$m�� 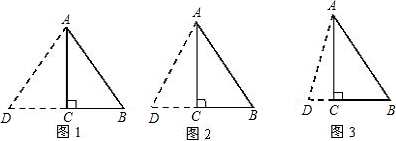
���� ������Ҫ����Թ��ɶ��������������ε����ʵ�֪ʶ�����������գ���ͨ������������������ε���������ǽ����Ĺؼ���

��ϰ��ϵ�д�
 ��ѧ��ʦ����ϵ�д�
��ѧ��ʦ����ϵ�д�
�����Ŀ
1���������x��yͬʱ����10������ô���з�ʽ��ֵ��С10�����ǣ�������
| A�� | $\frac{x-1}{y-1}$ | B�� | $\frac{x+1}{y+1}$ | C�� | $\frac{x^2}{y^3}$ | D�� | $\frac{x}{x+y}$ |
18����֪x=2-$\sqrt{3}$�������ʽ$��{x}^{2}+��2+\sqrt{3}��x+4\sqrt{3}$��ֵ�ǣ�������
| A�� | 8 | B�� | 8$\sqrt{3}$ | C�� | 2$+\sqrt{3}$ | D�� | 7 |
 ��ͼ����֪��ABC�ա�ADE����D��BC�ϣ���ABC=60�㣬��C=45�㣬���ADE�ɿ������ɡ�ABC�ض���A��ʱ����ת60�ȵõ��ģ�
��ͼ����֪��ABC�ա�ADE����D��BC�ϣ���ABC=60�㣬��C=45�㣬���ADE�ɿ������ɡ�ABC�ض���A��ʱ����ת60�ȵõ��ģ�