题目内容
15.计算:(1)$\frac{1}{3}$×$\sqrt{0.36}$+$\frac{1}{5}$×$\sqrt{900}$-($\sqrt{1+\frac{9}{16}}$-$\sqrt{2.25}$)$\frac{1}{3}$
(2)|1-$\sqrt{2}$|+|$\sqrt{2}-\sqrt{3}$|+|$\sqrt{3}$-2|
(3)x2•(x2)3÷x5
(4)-3xy2z•(x2y)2
(5)x(x2-1)+2x2(x+1)-3x(2x-5)
(6)(a+b)2-(a-b)2.
分析 (1)直接化简二次根式进而求出答案;
(2)直接利用绝对值的性质化简进而求出答案;
(3)直接利用幂的乘方运算法则以及同底数幂的乘除法运算法则求出答案;
(4)直接利用积的乘方运算法则以及同底数幂的乘法运算法则求出答案;
(5)直接去括号,再合并同类项求出答案;
(6)直接利用完全平方公式去括号,进而合并同类项求出答案.
解答 解:(1)$\frac{1}{3}$×$\sqrt{0.36}$+$\frac{1}{5}$×$\sqrt{900}$-($\sqrt{1+\frac{9}{16}}$-$\sqrt{2.25}$)$\frac{1}{3}$
=0.2+6-($\frac{5}{4}$-1.5)×$\frac{1}{3}$
=6$\frac{17}{60}$;
(2)|1-$\sqrt{2}$|+|$\sqrt{2}-\sqrt{3}$|+|$\sqrt{3}$-2|
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+2-$\sqrt{3}$
=1;
(3)x2•(x2)3÷x5
=x2•x6÷x5
=x3;
(4)-3xy2z•(x2y)2
=-3xy2z•x4y2
=-3x5y4z;
(5)x(x2-1)+2x2(x+1)-3x(2x-5)
=x3-x+2x3+2x2-6x2+15x
=3x3-4x2+14x;
(6)(a+b)2-(a-b)2
=a2+2ab+b2-(a2-2ab+b2)
=4ab.
点评 此题主要考查了整式的混合运算以及积的乘方运算法则和幂的乘方运算等知识,熟练掌握运算法则是解题关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
3. 如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )
如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )
 如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )
如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )| A. | 12cm | B. | 10cm | C. | 8cm | D. | 6cm |
10.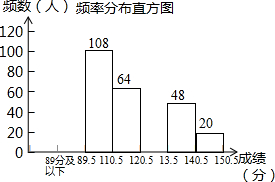 某县为调查九年级15000名学生“一模”考试的数学成绩的分布情况,抽取了400名学生的数学成绩(成绩得分皆为整数,满分150分)进行统计:
某县为调查九年级15000名学生“一模”考试的数学成绩的分布情况,抽取了400名学生的数学成绩(成绩得分皆为整数,满分150分)进行统计:
频率分布表
请你根据不完整的频率分布表,解答下列问题:
(1)补全频率分布表;
(2)补全频数分布直方图;
(3)若将得分转化为等级,规定得分“89分及以下”分评为“D”,“89.5-110.5分”评为“C”,“110.5-130.5扥”评为“B”,“130.5-150.5分”评为“A”,这次15000名学生中约有多少人评为“D”?如果随机抽取一名学生的成绩等级,则这名学生的成绩评为“A”、“B”、“C”、“D”哪一个等级的可能性大?请说明理由.
 某县为调查九年级15000名学生“一模”考试的数学成绩的分布情况,抽取了400名学生的数学成绩(成绩得分皆为整数,满分150分)进行统计:
某县为调查九年级15000名学生“一模”考试的数学成绩的分布情况,抽取了400名学生的数学成绩(成绩得分皆为整数,满分150分)进行统计:频率分布表
| 分组 | 频数 | 频率 |
| 89分及以下 | ||
| 89.5-110.5 | 108 | |
| 110.5-120.5 | 64 | 0.16 |
| 120.5-130.5 | 0.20 | |
| 130.5-140.5 | 48 | |
| 140.5-150.5 | 20 | 0.05 |
| 合计 | 400 | 1 |
(1)补全频率分布表;
(2)补全频数分布直方图;
(3)若将得分转化为等级,规定得分“89分及以下”分评为“D”,“89.5-110.5分”评为“C”,“110.5-130.5扥”评为“B”,“130.5-150.5分”评为“A”,这次15000名学生中约有多少人评为“D”?如果随机抽取一名学生的成绩等级,则这名学生的成绩评为“A”、“B”、“C”、“D”哪一个等级的可能性大?请说明理由.
20.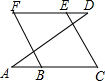 如图,能够判断FB∥CE的条件是( )
如图,能够判断FB∥CE的条件是( )
 如图,能够判断FB∥CE的条件是( )
如图,能够判断FB∥CE的条件是( )| A. | ∠F+∠C=180° | B. | ∠ABF=∠C | C. | ∠F=∠C | D. | ∠A=∠D |
4.下列计算错误的是( )
| A. | a8÷a4=a4 | B. | (-a)5÷(-a)4=-a | C. | (-a)5÷(-a4)=a | D. | (b-a)3÷(a-b)2=a-b |
5. 如图,PA、PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=5O°,则∠ACB的大小是( )
如图,PA、PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=5O°,则∠ACB的大小是( )
 如图,PA、PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=5O°,则∠ACB的大小是( )
如图,PA、PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=5O°,则∠ACB的大小是( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
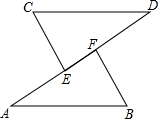 如图所示,AB∥CD,∠CEA=3∠A,∠BFD=3∠D,试说明:CE∥BF.
如图所示,AB∥CD,∠CEA=3∠A,∠BFD=3∠D,试说明:CE∥BF.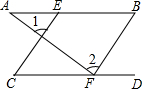 如图,已知∠1=∠2,∠B=∠C,试说明AB∥CD.
如图,已知∠1=∠2,∠B=∠C,试说明AB∥CD.