题目内容
6. 如图,点P是△ABC外的一点,PD⊥AB于点D,PE⊥AC于点E,PF⊥BC于点F,连接PB,PC.若PD=PE=PF,∠BAC=70°,则∠BPC的度数为35°.
如图,点P是△ABC外的一点,PD⊥AB于点D,PE⊥AC于点E,PF⊥BC于点F,连接PB,PC.若PD=PE=PF,∠BAC=70°,则∠BPC的度数为35°.
分析 根据角平分线的判定,可得∠ABP=∠CBP,∠ACP=∠FCP;根据三角形外角的性质,可得∠ABC+∠BAC=∠ACF,∠PBC+∠BPC=∠FCP,根据等量代换,可得答案.
解答 解:由PD⊥AB于点D,PE⊥AC于点E,PF⊥BC于点F,连接PB,PC.若PD=PE=PF,得
∠ABP=∠CBP,∠ACP=∠FCP.
由∠ACF是△ABC的外角,得
∠ABC+∠BAC=∠ACF.
两边都除以2,得
$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠BAC=$\frac{1}{2}$∠ACF,
即∠PBC+$\frac{1}{2}$∠BAC=∠FCP.
由∠PCF是△BCP的外角,得
∠PBC+∠BPC=∠FCP,
∴∠BPC=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×70°=35°,
故答案为:35°.
点评 本题考查了角平分线的判定,利用了角平分线的判定,三角形外角的性质,利用角平分线的判定得出∠ABP=∠CBP,∠ACP=∠FCP是解题关键.

练习册系列答案
相关题目
17.已知方程:①$\frac{x+3}{2}$-$\frac{2x+3}{3}$=$\frac{3x+11}{6}$;②$\frac{x}{2}$=x+1;③4x-3=5x+1;④3(x+5)-7x=2(3-2x)+9
其中有相同解的是( )
其中有相同解的是( )
| A. | ①② | B. | ①②③ | C. | ①③ | D. | ①②④ |
11.为了解决药品价格过高的问题,决定大幅度降低药品的价格,其中将原价a元的某种常用药降价40%,则降价后此药价格为( )
| A. | $\frac{a}{0.4}$元 | B. | $\frac{a}{0.6}$元 | C. | 60%a元 | D. | 40%a 元 |
15.$\sqrt{4}$的算术平方根是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 4 | D. | 16 |
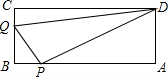 如图.A、B、C、D为矩形的4个顶点:AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达点B为止:点Q以2cm/s的速度向点B移动,经过多长时间P、Q两点之间的距离是10cm?
如图.A、B、C、D为矩形的4个顶点:AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达点B为止:点Q以2cm/s的速度向点B移动,经过多长时间P、Q两点之间的距离是10cm?