题目内容
11.某商店购进一种商品,单价为每件20元,试销中发现这种商品每天的销售量y(件)与每件的销售价x(元)满足关系:y=80-2x,每天的销售利润为w(元)①若想每天获得150的利润,则销售价应定为每件多少元?
②写出w与y之间的函数关系式;
③若规定试销期间销售单价不低于成本单价,且获利不得高于成本的40%,则销售单价定位每件多少元时,可获得最大利润?最大利润为多少元?
分析 ①利用等量关系:利润150=每件商品的利润×卖出的件数=(售价-进价)×卖出的件数,列出方程解答即可;
②利用总利润=每件商品的利润×卖出的件数列出函数关系式即可;
③得出自变量的取值范围,应用二次函数的性质,求最大值即可.
解答 解:①由题意得(x-20)(80-2x)=150,
解得:x1=35,x2=25.
答:销售价应定为每件25元或35元时,可获得150的利润.
②w=(x-20)(80-2x)=-2x2+120x-1600;
③由获利不得高于成本的40%可知:
20≤x≤28,
函数w=-2x2+120x-1600的对称轴x=-$\frac{120}{2×(-2)}$=30,
∵a=-2<0,抛物线开口向下,
∴当x<30时,w随着x的增大而增大,
∴当x=28时,
w的最大值为-2×282+120×28-1600=192元.
即销售单价定位每件28元时,可获得最大利润;最大利润为192元.
点评 本题考查了二次函数的应用,解题的关键是从实际问题中整理出二次函数模型,并运用二次函数的知识解决实际问题.

练习册系列答案
相关题目
2.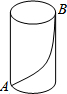 如图,一只蚂蚁从点A沿圆柱表面爬到点B,如果圆柱的高为8cm,圆柱的底面半径为$\frac{6}{π}$cm,那么最短的路线长是( )
如图,一只蚂蚁从点A沿圆柱表面爬到点B,如果圆柱的高为8cm,圆柱的底面半径为$\frac{6}{π}$cm,那么最短的路线长是( )
 如图,一只蚂蚁从点A沿圆柱表面爬到点B,如果圆柱的高为8cm,圆柱的底面半径为$\frac{6}{π}$cm,那么最短的路线长是( )
如图,一只蚂蚁从点A沿圆柱表面爬到点B,如果圆柱的高为8cm,圆柱的底面半径为$\frac{6}{π}$cm,那么最短的路线长是( )| A. | 6cm | B. | 8cm | C. | 10cm | D. | 10πcm |
 如图,已知AB∥CD,EA是∠CEB的平分线,若∠BED=40°,则∠A的度数是70°.
如图,已知AB∥CD,EA是∠CEB的平分线,若∠BED=40°,则∠A的度数是70°.
 有增根,则m=________
有增根,则m=________ 是方程
是方程 的两根,则
的两根,则 的值是( )
的值是( ) D.
D. 