题目内容
12.已知x,y满足|x-2|+$\sqrt{y+1}$=0,求代数式[(x2+y2)-(x-y)2+2y(2x-y)]÷4y的值.分析 原式中括号中利用完全平方公式及单项式乘以多项式法则计算,合并后利用多项式除以单项式法则计算得到最简结果,利用非负数的性质求出x与y的值,代入计算即可求出值.
解答 解:原式=(x2+y2-x2+2xy-y2+4xy-2y2)÷4y=(6xy-2y2)÷4y=$\frac{3}{2}$x-$\frac{1}{2}$y,
∵|x-2|+$\sqrt{y+1}$=0,
∴x=2,y=-1,
则原式=3$\frac{1}{2}$.
点评 此题考查了整式的混合运算,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.下列函数关系中,是二次函数的是( )
| A. | 在弹性限度内,弹簧的长度y与所挂物体的质量x之间的关系 | |
| B. | 当距离一定时,汽车行驶的时间t与速度v之间的关系 | |
| C. | 矩形的面积S和矩形的宽x之间的关系 | |
| D. | 等边三角形的面积S与边长x之间的关系 |
2.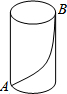 如图,一只蚂蚁从点A沿圆柱表面爬到点B,如果圆柱的高为8cm,圆柱的底面半径为$\frac{6}{π}$cm,那么最短的路线长是( )
如图,一只蚂蚁从点A沿圆柱表面爬到点B,如果圆柱的高为8cm,圆柱的底面半径为$\frac{6}{π}$cm,那么最短的路线长是( )
 如图,一只蚂蚁从点A沿圆柱表面爬到点B,如果圆柱的高为8cm,圆柱的底面半径为$\frac{6}{π}$cm,那么最短的路线长是( )
如图,一只蚂蚁从点A沿圆柱表面爬到点B,如果圆柱的高为8cm,圆柱的底面半径为$\frac{6}{π}$cm,那么最短的路线长是( )| A. | 6cm | B. | 8cm | C. | 10cm | D. | 10πcm |
 如图,已知AB∥CD,EA是∠CEB的平分线,若∠BED=40°,则∠A的度数是70°.
如图,已知AB∥CD,EA是∠CEB的平分线,若∠BED=40°,则∠A的度数是70°.