题目内容
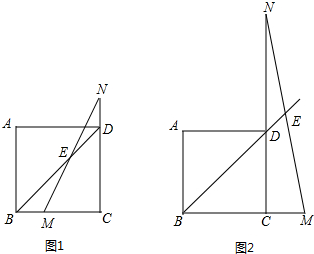
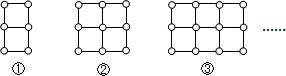
14. 如图,已知∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,DE=1.7cm,BE=0.8cm,求线段AD的长.
如图,已知∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,DE=1.7cm,BE=0.8cm,求线段AD的长.
分析 求出∠E=∠ADC=90°,∠BCE=∠CAD,证△BCE≌△ACD,推出CD=BE=0.8cm,AD=CE,即可得出答案
解答 解:∵BE⊥CE,AD⊥CE,∠ACB=90°,
∴∠E=∠ADC=∠ACB=90°,
∴∠BCE+∠ACD=90°,∠CAD+∠ACD=90°,
∴∠BCE=∠CAD,
在△BCE和△ACD中
$\left\{\begin{array}{l}{∠E=∠ADC}\\{∠BCE=∠CAD}\\{BC=AC}\end{array}\right.$
∴△BCE≌△ACD,
∴CD=BE=0.8cm,AD=CE,
∴AD=CE=CD+DE=BE+DE=0.8+1.7=2.5cm.
点评 本题考查了全等三角形的性质和判定的应用,解此题的关键是求出△BCE≌△ACD.

练习册系列答案
相关题目
4.下列函数关系中,是二次函数的是( )
| A. | 在弹性限度内,弹簧的长度y与所挂物体的质量x之间的关系 | |
| B. | 当距离一定时,汽车行驶的时间t与速度v之间的关系 | |
| C. | 矩形的面积S和矩形的宽x之间的关系 | |
| D. | 等边三角形的面积S与边长x之间的关系 |
2.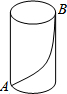 如图,一只蚂蚁从点A沿圆柱表面爬到点B,如果圆柱的高为8cm,圆柱的底面半径为$\frac{6}{π}$cm,那么最短的路线长是( )
如图,一只蚂蚁从点A沿圆柱表面爬到点B,如果圆柱的高为8cm,圆柱的底面半径为$\frac{6}{π}$cm,那么最短的路线长是( )
 如图,一只蚂蚁从点A沿圆柱表面爬到点B,如果圆柱的高为8cm,圆柱的底面半径为$\frac{6}{π}$cm,那么最短的路线长是( )
如图,一只蚂蚁从点A沿圆柱表面爬到点B,如果圆柱的高为8cm,圆柱的底面半径为$\frac{6}{π}$cm,那么最短的路线长是( )| A. | 6cm | B. | 8cm | C. | 10cm | D. | 10πcm |