题目内容
观察式子: =
= (1-
(1- ),
),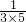 =
= (
( -
- ),
),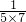 =
= (
( -
- ),….由此计算:
),….由此计算: +
+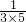 +
+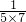 +…+
+…+ =________.
=________.
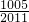
分析:根据所给式子,发现规律:
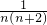 =
= (
( ),然后运用抵消的方法进行计算.
),然后运用抵消的方法进行计算.解答:原式=
 (1-
(1- +
+ -
- +…+
+…+ -
- )=
)= ×(1-
×(1- )=
)= ×
× =
=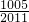 .
.点评:计算此类题的时候,要善于找到拆分的规律,然后运用抵消的方法简便计算.

练习册系列答案
相关题目