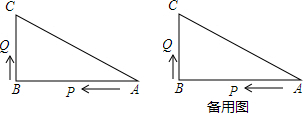
题目内容
7. 如图,在矩形ABCD中,AB=4,AD=$\sqrt{3}$,点E是AB的中点,将线段DC以每秒1个单位长度的速度沿射线DC方向平移至D′C′,设移动时间为t秒,连接D′E并延长,交C′B的延长线于点F,连接AF.
如图,在矩形ABCD中,AB=4,AD=$\sqrt{3}$,点E是AB的中点,将线段DC以每秒1个单位长度的速度沿射线DC方向平移至D′C′,设移动时间为t秒,连接D′E并延长,交C′B的延长线于点F,连接AF.(1)当t=1时,求BC′的长;
(2)证明:四边形AFBD′是平行四边形;
(3)当四边形AFBD′是菱形时,求t的值.
分析 (1)首先证明DD′=CC′=1,再利用勾股定理即可解决问题.
(2)欲证明四边形AFBD′是平行四边形,只要证明ED′=EF,利用平行线分线段成比例定理即可证明.
(3)当FD′⊥AB时四边形AFBD′是菱形,求出DD′即可解决问题.
解答 解:(1)t=1时,DD′=1,
∵CD=C′D′,
∴CC′=DD′=1,
∵四边形ABCD是矩形,
∴AD=BC=$\sqrt{3}$,∠BCD=∠BCC′=90°,
∴BC′=$\sqrt{B{C}^{2}+CC{′}^{2}}$=$\sqrt{(\sqrt{3})^{2}+{1}^{2}}$=2.
(2)∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,'
∵AE=EB,EB∥C′D′,
∴$\frac{FE}{FD′}$=$\frac{EB}{C′D′}$,
∵C′D′=CD=AB,
∴$\frac{FE}{FD′}$=$\frac{1}{2}$,
∴ED′=EF,∵AE=EB,
∴四边形AFBD′是平行四边形.
(3)∵四边形AFBD′是平行四边形,
∴当D′F⊥AB时,四边形AFBD′是菱形,
∵∠D=∠DAB=∠AED′=90°,
∴四边形AED′D是矩形,
∴DD′=AE=2,
∴t=2,
∴t=2时四边形AFBD′是菱形时.
点评 本题考查四边形综合题、平行四边形的判定和性质、矩形的性质、菱形的判定和性质、勾股定理、平行线分线段成比例定理等知识,解题的关键是灵活应用这些知识解决问题,证明E是FD′中点是解题的突破口,属于中考常考题型.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
3.丽水市某一周每天的最高气温统计如下(单位:℃):24,26,28,30,28,28,26,则这组数据的众数与中位数分别是( )
| A. | 28,30 | B. | 28,28 | C. | 28,26 | D. | 26,28 |
12.下列实数中,是无理数的是( )
| A. | $\frac{1}{7}$ | B. | $\sqrt{9}$ | C. | $\root{3}{27}$ | D. | $\frac{π}{3}$ |
19. 如图,在四边形ABCD中,∠C=110°,与∠BAD,∠ABC相邻的外角都是120°,则∠ADC的外角α的度数是( )
如图,在四边形ABCD中,∠C=110°,与∠BAD,∠ABC相邻的外角都是120°,则∠ADC的外角α的度数是( )
 如图,在四边形ABCD中,∠C=110°,与∠BAD,∠ABC相邻的外角都是120°,则∠ADC的外角α的度数是( )
如图,在四边形ABCD中,∠C=110°,与∠BAD,∠ABC相邻的外角都是120°,则∠ADC的外角α的度数是( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
15.若x>y,则下列式子中错误的是( )
| A. | x-2>y-2 | B. | x+3>y+3 | C. | $\frac{x}{3}$>$\frac{y}{3}$ | D. | -5x>-5y |
 如图,梯形BCDE中,DE∥BC,CD、BE的延长线交于点A,联结BD、CE相交于点O,已知AE=3,EB=6,DE=2.
如图,梯形BCDE中,DE∥BC,CD、BE的延长线交于点A,联结BD、CE相交于点O,已知AE=3,EB=6,DE=2.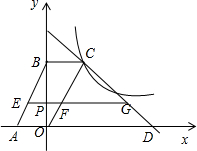 如图,在平面直角坐标系中,四边形ABCO是平行四边形,点O为坐标原点,点A的坐标为(-2,0),点B在y轴的正半轴上,点C在双曲线y=-$\frac{8}{x}$上,直线y=-x+m经过点C,交x轴于点D.
如图,在平面直角坐标系中,四边形ABCO是平行四边形,点O为坐标原点,点A的坐标为(-2,0),点B在y轴的正半轴上,点C在双曲线y=-$\frac{8}{x}$上,直线y=-x+m经过点C,交x轴于点D.