Question

7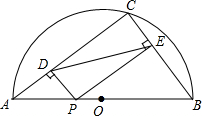．如图，AB是半⊙O的直径，点C是半⊙O上的一点，且AC=4cm，BC=3cm．点P是AB上的动点，过点P分别作PD⊥AC，PE⊥BC，垂足分别为点D、E，连接DE，则在点P移动过程中，DE的最小值为$\frac{12}{5}$cm．

Answer 1

分析 连接PC，证四边形PDCE是矩形得DE=PC，即可知当CP⊥AB时CP=DE取得最小值，根据S_△ABC=$\frac{1}{2}$AC•CB=$\frac{1}{2}$AB•CP′得CP′=$\frac{AC•CB}{AB}$=$\frac{12}{5}$，即可知答案．

解答 解：如图，连接PC，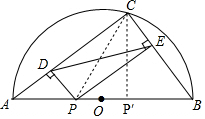

∵AB为⊙O的直径，
∴∠ACB=90°，
∵AC=4cm，BC=3cm，
∴AB=5cm，
又∵PD⊥AC，PE⊥BC，
∴∠PDC=∠ACB=∠PEC=90°，
∴四边形PDCE是矩形，
∴DE=PC，
当CP⊥AB时，CP=DE取得最小值，
∵S_△ABC=$\frac{1}{2}$AC•CB=$\frac{1}{2}$AB•CP′，
∴CP′=$\frac{AC•CB}{AB}$=$\frac{12}{5}$，
故答案为：$\frac{12}{5}$cm．

点评 本题主要考查圆周角定理、勾股定理、矩形的判定与性质及三角形的面积，证得四边形PDCE是矩形得DE=PC，从而知当CP⊥AB时CP=DE取得最小值是解题的关键．