题目内容
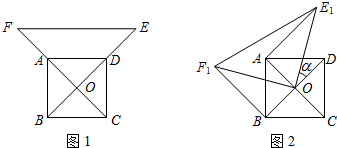
9.回顾旧知:在探究有关正多边形的有关性质时,我们是从那几个方面展开的?探究的方法与过程又是怎样的?(不要求回答)温馨提示,如图1,是一个边长为a的正六边形.我们知道它具有如下的性质:①正六边形的每条边长度相等;②正六边形的六个内角相等,都是120°;③正六边形的内角和为720°;④正六边形的外角和为360°.等.
解答问题:
(1)观察图2,请你在下面的横线上,再写出边长为a的正六边形所具有不同于上述的性质(不少于5条):答案不唯一.
(2)尺规作图:在图2中作出圆内接正六边形的内切圆(不要求写作法,只保留作图痕迹);
(3)求出这个正六边形外接圆半径与内切圆半径的比值.

分析 (1)直接利用正六边形的性质以及结合正多边形和圆的性质分别得出即可;
(2)利用正六边形的内切圆得出其边心距即内切圆的半径,即可得出答案;
(3)求出正六边形内切圆的半径进而得出答案.
解答 解:(1)①正六边形既是轴对称图形,又是中心对称图形;
②正六边形的面积为:$\frac{3\sqrt{3}}{2}$a2,周长为6a;
③正六边形有一个内切圆、外接圆,它们是同心圆;
④圆内接正六边形的每条边在圆内所对的优弧长度相等;
⑤圆内接正六边形的每条边在圆内所对的优弧的弧度相等;
⑥圆内接正六边形的每条边(或说弦)在圆内所对的劣弧的长度相等;
⑦圆内接正六边形的每条边(或说弦)在圆内所对的劣弧的弧度相等;
⑧圆内接正六边形的每条边(或说弦)在圆内所对的圆心角(中心角)相等,都是60°;
⑨圆内接正六边形的边长等于圆的半径;
⑩圆内接正六边形的边心距为:$\frac{\sqrt{3}}{2}$a等.
(2)如图2所示:
(3)如图2,连结EO,在Rt△ONE中,
∵OE=DE=a,
∠EON=$\frac{1}{2}$DOE=30°,
∴OE=$\frac{\sqrt{3}}{2}$a,
∴边长为a正六边形外接圆半径与内切圆半径的比值为:$\frac{a}{\frac{\sqrt{3}}{2}a}$=$\frac{2\sqrt{3}}{3}$.
点评 此题主要考查了正多边形和圆以及正六边形的性质,正确掌握正六边形的性质是解题关键.

练习册系列答案
相关题目
14.某年级有四个班,人数分别为:一班25人,二班22人,三班27人,四班26人.在一次考试中,四个班的班级平均分依次为81分,75分,89分,78分,则这次考试的年级平均分为( )
| A. | 79.25分 | B. | 80.75分 | C. | 81.06分 | D. | 82.53分 |
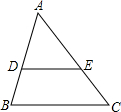 如图,已知$\frac{AD}{BD}$=$\frac{AE}{EC}$=$\frac{3}{2}$,试求$\frac{DE}{BC}$的值.
如图,已知$\frac{AD}{BD}$=$\frac{AE}{EC}$=$\frac{3}{2}$,试求$\frac{DE}{BC}$的值.