题目内容
已知关于x的方程x2-5x+a-1=0的一根大于3,另一根小于-1,求a的取值范围.
考点:一元二次方程根的分布
专题:
分析:可令f(x)=x2-5x+a-1,由方程x2-5x+a-1=0的一根小于-1,另一根大于3,可得
,解此不等式组即可得实数m的取值范围,即可解得a的范围
|
解答:解:方程x2-5x+a-1的一根小于-1,另一根大于3,
令f(x)=x2-5x+a-1则有
,
即
解得a<-5,
又∵△=25-4(a-1)>0,
∴a<
,
∴a<-5,
即a的取值范围是a<-5.
令f(x)=x2-5x+a-1则有
|
即
|
解得a<-5,
又∵△=25-4(a-1)>0,
∴a<
| 29 |
| 4 |
∴a<-5,
即a的取值范围是a<-5.
点评:本题的考点是一元二次方程的根的分布与系数的关系,解题的关键是理解根的分布与方程相应函数的函数值的对应关系,由此得到参数所满足的不等式,解出符合条件的参数的取值范围.本题考察了转化的思想及推理判断的能力.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 如图要使图形与自身重合至少需旋转( )
如图要使图形与自身重合至少需旋转( )| A、45° | B、60° |
| C、90° | D、120° |
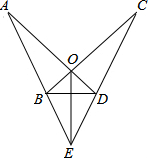 如图,AD与BC相交于点O,OA=OC,∠A=∠C,BE=DE.求证:OE垂直平分BD.
如图,AD与BC相交于点O,OA=OC,∠A=∠C,BE=DE.求证:OE垂直平分BD.