题目内容
19.已知α,β是关于x的方程x2-3x+k=0的两个不等实根.(1)用k表示$\frac{β}{α}+\frac{α}{β}$;
(2)用k表示$\frac{4k-5}{2α-1}+\frac{k+18}{α+2β}+\frac{1}{3}{α^2}$.
分析 (1)由α,β是关于x的方程x2-3x+k=0的两个不等实根,于是得到α+β=3,αβ=k,代入代数式即可得到结果;
(2)根据α+β=3,αβ=k,于是得到α+2β=β+3,k+18=αβ+9+3α+3β=α(β+3)+3(β+3),$\frac{k+18}{α+2β}$=α+3,根据方程根的定义得到α2=3α-k,代入代数式化简后即可得到结论.
解答 解:(1)∵α,β是关于x的方程x2-3x+k=0的两个不等实根,
∴α+β=3,αβ=k,
∴(1)$\frac{β}{α}+\frac{α}{β}$=$\frac{(α+β)^2}{αβ}$-2=$\frac{9}{k}$-2;
(2)∵α+2β=β+3,k+18=αβ+9+3α+3β=α(β+3)+3(β+3),
∴$\frac{k+18}{α+2β}$=α+3,
∵α2=3α-k,
∴$\frac{4k-5}{2α-1}+\frac{k+18}{α+2β}+\frac{1}{3}{α^2}$=$\frac{4k-5}{2α-1}+\frac{k+18}{3+β}+\frac{1}{3}{α^2}$=$\frac{4k-5}{2α-1}$+(3+α)$+\frac{1}{3}{α}^{2}$=$\frac{3(4k-5)+3(2α-1)(3+α)+(3α-k)}{3(2α-1)}$=$\frac{48α-24-2αk+k}{3(2α-1)}$=$\frac{24(2α-1)-k(2α-1)}{3(2α-1)}$
=$\frac{24-k}{3}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

 阅读快车系列答案
阅读快车系列答案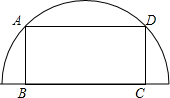 如图,一个长为2、宽为1的矩形ABCD内接于半圆O,矩形的长BC在半圆半径上,则半圆O的面积为( )
如图,一个长为2、宽为1的矩形ABCD内接于半圆O,矩形的长BC在半圆半径上,则半圆O的面积为( )| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | π | D. | 2π |
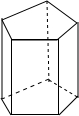 如图所示的五棱柱的底面边长都是5cm,侧棱长12cm,它有多少个面?它的所有侧面的面积之和是多少?
如图所示的五棱柱的底面边长都是5cm,侧棱长12cm,它有多少个面?它的所有侧面的面积之和是多少?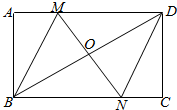 如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连BM,DN.
如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连BM,DN. 如图,是一个几何体从正面、左面、上面看得到的平面图形,判断下面说法的正误(正确的在括号内划△,错误的在括号内划▲)
如图,是一个几何体从正面、左面、上面看得到的平面图形,判断下面说法的正误(正确的在括号内划△,错误的在括号内划▲)