题目内容
19.(1)已知:x=$\frac{2}{{\sqrt{3}-1}}$,求x2-x+1的值.(2)已知:y=$\sqrt{1-8x}+\sqrt{8x-1}+\frac{1}{2}$,求代数式$\sqrt{\frac{x}{y}+\frac{y}{x}+2}-\sqrt{\frac{x}{y}+\frac{y}{x}-2}$的值.
分析 (1)先化简x=$\frac{2}{{\sqrt{3}-1}}$=$\sqrt{3}$+1,再进一步代入代数式求得答案即可;
(2)由二次根式的意义可知,1-8x≥0,8x-1≥0,先求得x,再进一步得出y,再进一步整理代数式求得答案即可.
解答 解:(1)∵x=$\frac{2}{{\sqrt{3}-1}}$=$\sqrt{3}$+1,
∴x2-x+1
=($\sqrt{3}$+1)2-($\sqrt{3}$+1)+1
=4+2$\sqrt{3}$-$\sqrt{3}$-1+1
=4+$\sqrt{3}$;
(2)∵1-8x≥0,8x-1≥0,
∴x=$\frac{1}{8}$,则y=$\frac{1}{2}$,
∴$\sqrt{\frac{x}{y}+\frac{y}{x}+2}-\sqrt{\frac{x}{y}+\frac{y}{x}-2}$
=$\frac{x+y}{\sqrt{xy}}$-$\frac{y-x}{\sqrt{xy}}$
=$\frac{2x}{\sqrt{xy}}$
=1.
点评 此题考查二次根式的化简求值,二次根式的意义,注意先把二次根式化简,再进一步代入球的数值.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
9.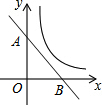 如图,直线y=k1x+b与坐标轴分别交于A(0,4),B(4,0)两点,反比例函数y=$\frac{{k}_{2}}{x}$的图象在第一象限,当这两个函数图象有公共点时,k2的最大整数值为( )
如图,直线y=k1x+b与坐标轴分别交于A(0,4),B(4,0)两点,反比例函数y=$\frac{{k}_{2}}{x}$的图象在第一象限,当这两个函数图象有公共点时,k2的最大整数值为( )
 如图,直线y=k1x+b与坐标轴分别交于A(0,4),B(4,0)两点,反比例函数y=$\frac{{k}_{2}}{x}$的图象在第一象限,当这两个函数图象有公共点时,k2的最大整数值为( )
如图,直线y=k1x+b与坐标轴分别交于A(0,4),B(4,0)两点,反比例函数y=$\frac{{k}_{2}}{x}$的图象在第一象限,当这两个函数图象有公共点时,k2的最大整数值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
10.下列计算不正确的是( )
| A. | |-3|=3 | B. | (-$\frac{1}{4}$)2=$\frac{1}{16}$ | C. | -$\frac{5}{3}+\frac{1}{3}=-\frac{4}{3}$ | D. | $\sqrt{{{({-2})}^2}}$=-2 |
14.甲、乙两人每次都从五个数-2,-1,0,1,2中任取一个,分别记作(x,y),则这些坐标表示的点在直线y=x+1上的概率为( )
| A. | $\frac{4}{25}$ | B. | $\frac{8}{25}$ | C. | $\frac{9}{25}$ | D. | $\frac{2}{5}$ |
 如图,已知∠ABC、∠DEF,且AB∥DE,BC∥EF,∠B、∠E具有怎样的关系?说明理由.
如图,已知∠ABC、∠DEF,且AB∥DE,BC∥EF,∠B、∠E具有怎样的关系?说明理由.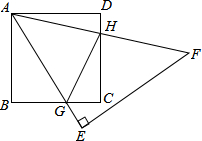 如图,已知正方形ABCD和等腰直角三角形△AEF,∠E=90°,AE和BC交于点G,AF和CD交于点H,正方形ABCD的面积为1cm2,则△CGH的周长为2.
如图,已知正方形ABCD和等腰直角三角形△AEF,∠E=90°,AE和BC交于点G,AF和CD交于点H,正方形ABCD的面积为1cm2,则△CGH的周长为2.