题目内容
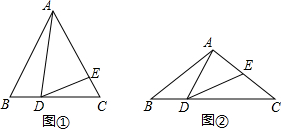
16. 如图,四边形ABCD中,∠A=∠C=90°,BF、DE分别平分∠ABC、∠ADC.判断BF、DE是否平行,并说明理由.
如图,四边形ABCD中,∠A=∠C=90°,BF、DE分别平分∠ABC、∠ADC.判断BF、DE是否平行,并说明理由.
分析 由题意可知∠ADC+∠ABC=180°,由BF、DE分别平分∠ABC、∠ADC可知:∠ADE+∠ABF=90°,又因为∠ADE+∠AED=90°,所以可得∠AED=∠ABF,即可得ED∥BF.
解答 解:ED∥BF;证明如下:
∵四边形ABCD中,∠A=∠C=90°,
∴∠ADC+∠ABC=180°,
∵BF、DE分别平分∠ABC、∠ADC,
∴∠ADC+∠ABC=2∠ADE+2∠ABF=180°,
∴∠ADE+∠ABF=90°,
又∵∠A=90°,∠ADE+∠AED=90°,
∴∠AED=∠ABF,
∴ED∥BF(同位角相等,两直线平行).
点评 本题考查了平行线的判定,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.此题还涉及到角平分线的性质,找到相应关系的角的解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列命题是真命题的是( )
| A. | 如果|a|=1那么a=1 | |
| B. | 同位角相等 | |
| C. | 对顶角相等 | |
| D. | 如一个数的绝对值等于它本身则这个数是正数 |
11.一根圆锥的主视图是等边三角形,边长为2,则这个圆锥的表面积为( )
| A. | 2π | B. | 3π | C. | $2\sqrt{3}$π | D. | $(1+2\sqrt{3}$)π |
 如图,点P沿半圆弧AB从A向B匀速运动,若运动时间为t,扇形OAP的面积为s,则s与t的函数图象大致是( )
如图,点P沿半圆弧AB从A向B匀速运动,若运动时间为t,扇形OAP的面积为s,则s与t的函数图象大致是( )