题目内容
20.以Rt△ABC的一条直角边AB为直径作圆,交斜边BC于E,F是AC的中点.求证:EF是⊙O的切线.分析 连接OE、AE,由AB是⊙O的直径,得到∠AEB=90°,推出∠CEA=90°.根据F为AC边上的中点,得到CF=FA=EF,根据等腰三角形的性质得到∠1=∠2,∠3=∠4,推出∠1+∠4=∠2+∠3,根据直角三角形的性质得到∠BAC=∠2+∠3=90°,于是得到∠FEO=∠1+∠4=90°.即可得到结论.
解答 证明: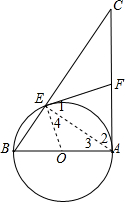 如图,连接OE、AE,
如图,连接OE、AE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠CEA=90°.
∵F为AC边上的中点,
∴CF=FA=EF,
∴∠1=∠2.
∵OA=OE,
∴∠3=∠4.
∴∠1+∠4=∠2+∠3.
∵在Rt△ABC中,∠BAC=∠2+∠3=90°,
∴∠FEO=∠1+∠4=90°.
∵E为⊙O上的点,
∴EF是⊙O的切线.
点评 主要考查了切线的判定方法,要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
10.下列方程中是一元二次方程的是( )
| A. | 3x2-2x+y=0 | B. | ax2+bx+c=0 | C. | (x-1)(x+2)=1 | D. | x2+$\frac{1}{{x}^{2}}$=0 |