题目内容
6. 如图,△ABC中,∠ACB=90°,AC=BC,D在BC上,BM⊥AD于M,求∠CMA的度数.
如图,△ABC中,∠ACB=90°,AC=BC,D在BC上,BM⊥AD于M,求∠CMA的度数.
分析 作CN⊥CM,与M交于一点N,证明△ACN≌△BCM,则CN=CM,则△MCN是等腰直角三角形,故∠CMA=45°.
解答 解:作CN⊥CM,交AM于N,
∵∠ACB=90°,
∴∠ACN=∠BCM,
∵∠CAN+∠ADC=∠MBC+∠BDM=90°,
∴∠CAN=∠MBC,
在△ACN和△BCM中,
$\left\{\begin{array}{l}{∠ACN=∠BCM}\\{AC=BC}\\{∠CAN=∠MBC}\end{array}\right.$,
∴△ACN≌△BCM,
∴CN=CM,
∴△MCN是等腰直角三角形,
∴∠CMA=45°.
点评 本题主要考查了全等三角形的判定与性质、等腰直角三角形的判定与性质,作辅助线构造全等三角形是解决问题的关键.

练习册系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,AC、BD相交于点E,S△ADE:S△ADC=1:3,那么S△ADE:S△CBE=1:4.
如图,在梯形ABCD中,AD∥BC,AC、BD相交于点E,S△ADE:S△ADC=1:3,那么S△ADE:S△CBE=1:4.
 在A和B之间有一条河,在BA延长线上取一点C,作BC的垂线AD和CE,点D位于BE上,测得AC=5米,CE=3.3米,AD=3米,求AB之间的距离.这个问题源于古希腊海伦《Dioptra》中的间接测量问题.
在A和B之间有一条河,在BA延长线上取一点C,作BC的垂线AD和CE,点D位于BE上,测得AC=5米,CE=3.3米,AD=3米,求AB之间的距离.这个问题源于古希腊海伦《Dioptra》中的间接测量问题.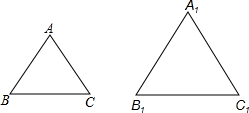 如图,在等腰△ABC和等腰△A1B1C1中,底边的长BC=4cm,B1C1=6cm,它们的周长分别为16cm和24cm,那么这两个等腰三角形的腰与底边是否成比例线段,说明理由.
如图,在等腰△ABC和等腰△A1B1C1中,底边的长BC=4cm,B1C1=6cm,它们的周长分别为16cm和24cm,那么这两个等腰三角形的腰与底边是否成比例线段,说明理由.