题目内容
19. 圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )| A. | 0.324πm2 | B. | 0.288πm2 | C. | 1.08πm2 | D. | 0.72πm2 |
分析 先根据AC⊥OB,BD⊥OB可得出△AOC∽△BOD,由相似三角形的对应边成比例可求出BD的长,进而得出BD′=0.3m,再由圆环的面积公式即可得出结论.
解答 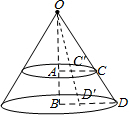 解:如图所示:∵AC⊥OB,BD⊥OB,
解:如图所示:∵AC⊥OB,BD⊥OB,
∴△AOC∽△BOD,
∴$\frac{OA}{OB}$=$\frac{AC}{BD}$,即$\frac{2}{3}$=$\frac{0.6}{BD}$,
解得:BD=0.9m,
同理可得:AC′=0.2m,则BD′=0.3m,
∴S圆环形阴影=0.92 π-0.32π=0.72π(m2).
故选:D.
点评 本题考查的是相似三角形的应用以及中心投影,利用相似三角形的对应边成比例得出阴影部分的半径是解题关键.

练习册系列答案
相关题目
10.计算3x3•(-2x2)的结果是( )
| A. | -6x5 | B. | -6x6 | C. | -x5 | D. | x5 |
14.在某校初三年级古诗词比赛中,初三(1)班60名学生的成绩统计如下:
则该班学生成绩的中位数和众数分别是( )
| 分数 | 50 | 60 | 70 | 80 | 90 | 100 |
| 人数 | 1 | 2 | 8 | 23 | 22 | 4 |
| A. | 80,80 | B. | 70,80 | C. | 80,90 | D. | 90,80 |
11.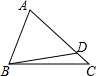 如图所示,点D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是( )
如图所示,点D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是( )
 如图所示,点D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是( )
如图所示,点D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是( )| A. | AC>BC | B. | AC=BC | C. | ∠A>∠ABC | D. | ∠A=∠ABC |
8.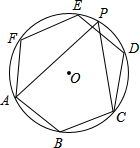 如图,正六边形ABCDEF内接于⊙O,点P为$\widehat{DE}$上一点,则tan∠APC的值为( )
如图,正六边形ABCDEF内接于⊙O,点P为$\widehat{DE}$上一点,则tan∠APC的值为( )
 如图,正六边形ABCDEF内接于⊙O,点P为$\widehat{DE}$上一点,则tan∠APC的值为( )
如图,正六边形ABCDEF内接于⊙O,点P为$\widehat{DE}$上一点,则tan∠APC的值为( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 1 |
9.为了了解居民节约用水情况,小明同学对本单元的住户当月用水量进行了调查,情况如表:
则关于这12户居民月用水量,下列说法错误的是( )
| 住户(户) | 2 | 4 | 5 | 1 |
| 月用水量(方/户) | 2 | 4 | 6 | 10 |
| A. | 平均数是5 | B. | 众数是6 | C. | 极差是8 | D. | 中位数是6 |
 小明上学途中要经过A,B两地,由于A,B两地之间有一片草坪,所以需要走路线AC,CB,如图,在△ABC中,AB=63m,∠A=45°,∠B=37°,求AC,CB的长.(结果保留小数点后一位)
小明上学途中要经过A,B两地,由于A,B两地之间有一片草坪,所以需要走路线AC,CB,如图,在△ABC中,AB=63m,∠A=45°,∠B=37°,求AC,CB的长.(结果保留小数点后一位)