题目内容
20．土家传统建筑的窗户上常有一些精致花纹、小辰对土家传统建筑非常感兴趣，他观察发现窗格的花纹排列呈现有一定规律，如图．其中“O”代表的就是精致的花纹，第1个图有5个花纹，第2个图有8个花纹，第3个图有11个花纹…，请问第7个图的精致花纹有（ ）
| A． | 26个 | B． | 23个 | C． | 20个 | D． | 17个 |
分析 观察图形可知从第二个图案开始，第加一扇窗户，就增加3个花纹．照此规律便可计算出第n个图形中花纹的个数，继而可得第7个图中花纹的个数．
解答 解：∵第一个图中有3+2=5个花纹；
第二个图中有2×3+2=8个花纹；
第三个图中有3×3+2=11个花纹；
…
∴第n个中有花纹（3n+2）个．
则第7个图中花纹的个数为3×7+2=23．
故选：B．
点评 本题考查的是图形变化的规律，解题的关键是明白每往后一幅图增加3个花纹．
练习册系列答案
阅读快车系列答案
相关题目
10．计算3x3•（-2x2）的结果是（ ）
| A． | -6x5 | B． | -6x6 | C． | -x5 | D． | x5 |
11．
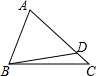如图所示，点D是△ABC的边AC上一点（不含端点），AD=BD，则下列结论正确的是（ ）
如图所示，点D是△ABC的边AC上一点（不含端点），AD=BD，则下列结论正确的是（ ）| A． | AC＞BC | B． | AC=BC | C． | ∠A＞∠ABC | D． | ∠A=∠ABC |
8．
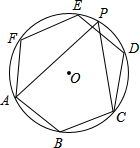如图，正六边形ABCDEF内接于⊙O，点P为$\widehat{DE}$上一点，则tan∠APC的值为（ ）
如图，正六边形ABCDEF内接于⊙O，点P为$\widehat{DE}$上一点，则tan∠APC的值为（ ）| A． | $\sqrt{3}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | 1 |
15．
如图，在△ABC中，D、E、F分别是边AB、AC、BC上的点，连接EF，CD相交于点G，若四边形BDEF是平行四边形，则下列说法不正确的是（ ）
如图，在△ABC中，D、E、F分别是边AB、AC、BC上的点，连接EF，CD相交于点G，若四边形BDEF是平行四边形，则下列说法不正确的是（ ）| A． | $\frac{AD}{DB}$=$\frac{DG}{CG}$ | B． | $\frac{AD}{DB}$=$\frac{EG}{GF}$ | C． | $\frac{AD}{DB}$=$\frac{BF}{BC}$ | D． | $\frac{AD}{DB}$=$\frac{DE}{FC}$ |
12．下列各数中，最小的数是（ ）
| A． | 3 | B． | 0 | C． | -2 | D． | -3 |
9．为了了解居民节约用水情况，小明同学对本单元的住户当月用水量进行了调查，情况如表：
则关于这12户居民月用水量，下列说法错误的是（ ）
| 住户（户） | 2 | 4 | 5 | 1 |
| 月用水量（方/户） | 2 | 4 | 6 | 10 |
| A． | 平均数是5 | B． | 众数是6 | C． | 极差是8 | D． | 中位数是6 |
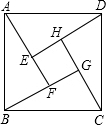如图示我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”，图中的四个直角三角形是全等的，如果大正方形ABCD的面积是小正方形EFGH面积的13倍，那么tan∠ADE的值为$\frac{2}{3}$．