题目内容
3.下列函数:①y=$\frac{1}{2}$x;②y=2-x;③y=$\frac{2}{x}$(x>0);④y=x2,
其中y的值随x值得增大而增大的有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 分别根据正比例函数的性质、一次函数的性质、反比例函数的性质及二次函数的性质对各小题进行逐一分析即可.
解答 解:①∵y=$\frac{1}{2}$x中,k=$\frac{1}{2}$>0,∴y随x的增大而增大,故本小题正确;
②∵y=2-x中,k=-1<0,∴y随x的增大而减小,故本小题错误;
③∵y=$\frac{2}{x}$(x>0)中,k=2>0,∴y随x的增大而减小,故本小题错误;
④∵y=x2中,k=1>0,∴在y轴左侧,y随x的增大而减小,故本小题错误.
故选D.
点评 本题考查的是反比例函数的性质,熟知反比例函数的增减性是解答此题的关键.

练习册系列答案
相关题目
13. 若一次函数y=kx+b的图象如图所示,则y<0时自变量x的取值范围是( )
若一次函数y=kx+b的图象如图所示,则y<0时自变量x的取值范围是( )
 若一次函数y=kx+b的图象如图所示,则y<0时自变量x的取值范围是( )
若一次函数y=kx+b的图象如图所示,则y<0时自变量x的取值范围是( )| A. | x>2 | B. | x<2 | C. | x>-1 | D. | x<-1 |
14.在某校初三年级古诗词比赛中,初三(1)班60名学生的成绩统计如下:
则该班学生成绩的中位数和众数分别是( )
| 分数 | 50 | 60 | 70 | 80 | 90 | 100 |
| 人数 | 1 | 2 | 8 | 23 | 22 | 4 |
| A. | 80,80 | B. | 70,80 | C. | 80,90 | D. | 90,80 |
11.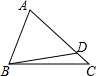 如图所示,点D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是( )
如图所示,点D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是( )
 如图所示,点D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是( )
如图所示,点D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是( )| A. | AC>BC | B. | AC=BC | C. | ∠A>∠ABC | D. | ∠A=∠ABC |
18.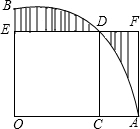 如图,扇形AOB的圆心角为直角,正方形OCDE的顶点C,E,D分别在OA,OB,弧AB上,过点A作AF⊥ED,交ED的延长线于点F,已知图中阴影部分的面积为$\sqrt{2}$-1,则正方形OCDE边长为( )
如图,扇形AOB的圆心角为直角,正方形OCDE的顶点C,E,D分别在OA,OB,弧AB上,过点A作AF⊥ED,交ED的延长线于点F,已知图中阴影部分的面积为$\sqrt{2}$-1,则正方形OCDE边长为( )
 如图,扇形AOB的圆心角为直角,正方形OCDE的顶点C,E,D分别在OA,OB,弧AB上,过点A作AF⊥ED,交ED的延长线于点F,已知图中阴影部分的面积为$\sqrt{2}$-1,则正方形OCDE边长为( )
如图,扇形AOB的圆心角为直角,正方形OCDE的顶点C,E,D分别在OA,OB,弧AB上,过点A作AF⊥ED,交ED的延长线于点F,已知图中阴影部分的面积为$\sqrt{2}$-1,则正方形OCDE边长为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
8.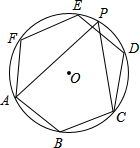 如图,正六边形ABCDEF内接于⊙O,点P为$\widehat{DE}$上一点,则tan∠APC的值为( )
如图,正六边形ABCDEF内接于⊙O,点P为$\widehat{DE}$上一点,则tan∠APC的值为( )
 如图,正六边形ABCDEF内接于⊙O,点P为$\widehat{DE}$上一点,则tan∠APC的值为( )
如图,正六边形ABCDEF内接于⊙O,点P为$\widehat{DE}$上一点,则tan∠APC的值为( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 1 |
15. 如图,在△ABC中,D、E、F分别是边AB、AC、BC上的点,连接EF,CD相交于点G,若四边形BDEF是平行四边形,则下列说法不正确的是( )
如图,在△ABC中,D、E、F分别是边AB、AC、BC上的点,连接EF,CD相交于点G,若四边形BDEF是平行四边形,则下列说法不正确的是( )
 如图,在△ABC中,D、E、F分别是边AB、AC、BC上的点,连接EF,CD相交于点G,若四边形BDEF是平行四边形,则下列说法不正确的是( )
如图,在△ABC中,D、E、F分别是边AB、AC、BC上的点,连接EF,CD相交于点G,若四边形BDEF是平行四边形,则下列说法不正确的是( )| A. | $\frac{AD}{DB}$=$\frac{DG}{CG}$ | B. | $\frac{AD}{DB}$=$\frac{EG}{GF}$ | C. | $\frac{AD}{DB}$=$\frac{BF}{BC}$ | D. | $\frac{AD}{DB}$=$\frac{DE}{FC}$ |
12.下列各数中,最小的数是( )
| A. | 3 | B. | 0 | C. | -2 | D. | -3 |
