题目内容
3.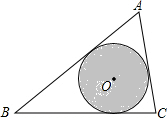 如图,△ABC中,AB=8,AC=5,∠A=60°,圆O是三角形的内切圆,如果在这个三角形内随意抛一粒豆子,则豆子落在圆O内的概率为$\frac{\sqrt{3}π}{10}$.
如图,△ABC中,AB=8,AC=5,∠A=60°,圆O是三角形的内切圆,如果在这个三角形内随意抛一粒豆子,则豆子落在圆O内的概率为$\frac{\sqrt{3}π}{10}$.
分析 作CD⊥AB于D,根据直角三角形的性质和勾股定理求出CD、AD的长,根据三角形的面积=$\frac{1}{2}$×(AB+BC+AC)×r计算即可,再根据概率=相应的面积与总面积之比即可求解.
解答 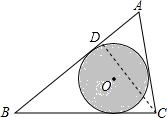 解:作CD⊥AB于D,
解:作CD⊥AB于D,
∵∠A=60°,
∴∠ACD=30°,
∴AD=$\frac{1}{2}$AC=$\frac{5}{2}$,
∴CD=$\frac{5\sqrt{3}}{2}$,BD=AB-CD=$\frac{11}{2}$,
∴BC=7,
设△ABC的内切圆半径为r,
$\frac{1}{2}$×(AB+BC+AC)×r=$\frac{1}{2}$×AB×CD,
解得r=$\sqrt{3}$,
$\frac{1}{2}$×AB×CD=$\frac{1}{2}$×8×$\frac{5\sqrt{3}}{2}$=10$\sqrt{3}$,
π×($\sqrt{3}$)2=π×3=3π,
豆子落在圆O内的概率为$\frac{3π}{10\sqrt{3}}$=$\frac{\sqrt{3}π}{10}$.
故答案为:$\frac{\sqrt{3}π}{10}$.
点评 本题考查的是几何概率,三角形内心的性质,掌握三角形的内心是三角形三条角平分线的交点和角平分线的性质是解题的关键.

练习册系列答案
相关题目

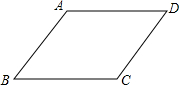 如图,平行四边形ABCD中,∠B=60°,AB=8cm,AD=10cm,点P在边BC上从B向C运动,点Q在边DA上从D向A运动,如果P,Q运动的速度都为每秒1cm,那么当运动时间t=7秒时,四边形ABPQ是直角梯形.
如图,平行四边形ABCD中,∠B=60°,AB=8cm,AD=10cm,点P在边BC上从B向C运动,点Q在边DA上从D向A运动,如果P,Q运动的速度都为每秒1cm,那么当运动时间t=7秒时,四边形ABPQ是直角梯形. 如图,将三角板的直角顶点放在直尺的一边上,若∠1=70°,则∠2的度数为20°.
如图,将三角板的直角顶点放在直尺的一边上,若∠1=70°,则∠2的度数为20°. 已知关于x的函数y=ax2-2abx+ab2-1,直线y=-ax+3与y轴交于点A,与x轴的正半轴交于点P,点B的纵坐标为3,且AP⊥BP,AP=BP.
已知关于x的函数y=ax2-2abx+ab2-1,直线y=-ax+3与y轴交于点A,与x轴的正半轴交于点P,点B的纵坐标为3,且AP⊥BP,AP=BP.
 小明带着自己家种的土豆到市场去卖,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出土豆的千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题:
小明带着自己家种的土豆到市场去卖,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出土豆的千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题: