题目内容
12.问题解决(1)如图1,△ABC中,经过点A的中线AD把△ABC分成△ASD和△ACD,则△ABD的面积S1等于△ACD的面积S2,请你说明理由:
问题应用
(2)如图2,△ABC中,D是BC的中点,F是AD的中点,△ABC的面积12,则△ABF的面积3;
问题拓展
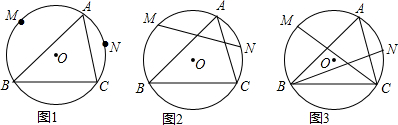
(3)如图3,四边形ABCD中,O是内部任意一点,点E、F、G、H分别是AD、AB、BC、CD边的中点,四边形AFOE的面积为3,四边形BGOF的面积为5,四边形CHOG的面积为4.求四边形DEOH的面积;
(4)如图4,边长为2正方形ABED与边长为2等腰直角三角形ABC拼合在一起.请你画出过点A作一条直线把四边形ADEC的面积分成相等的两部分.
分析 (1)过点A作AH⊥BC于点H;由三角形的面积公式得出△ABD的面积S1=$\frac{1}{2}$BD•AH,△ACD的面积S2=$\frac{1}{2}$CD•AH,由D为BC的中点 得出BD=CD,即可得出结论;
(2)由中点的性质得出△ABD的面积=$\frac{1}{2}$△ABC的面积=6,△ABF的面积=$\frac{1}{2}$△ABD的面积=3即可;
(3)连接OA、OB、OC、OD,设△AOE的面积为m,由中点的性质得出△AOE的面积=△DOE的面积=m,△AOF的面积=△BOF的面积,△BOG的面积=△COG的面积,△DOH的面积=△COH的面积,得出△AOF的面积=△BOF的面积=3-m,同理得:△BOG的面积=△COG的面积=2+m,△DOH的面积=△COH的面积=2-m,得出四边形DEOH的面积=△DOE的面积+△DOH的面积=2即可;
(4)连接AE,由已知条件得出△ABC的面积=$\frac{1}{2}$正方形ABED的面积=△ABE的面积=△ADE的面积,取BE的中点M,作直线AM,则△ABM的面积=△AEM的面积,∴△ACM的面积=四边形ADEM的面积即可.
解答 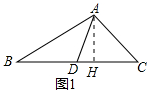 (1)证明:如图1,过点A作AH⊥BC于点H;
(1)证明:如图1,过点A作AH⊥BC于点H;
∵△ABD的面积S1=$\frac{1}{2}$BD•AH,△ACD的面积S2=$\frac{1}{2}$CD•AH,
又∵D为BC的中点,
∴BD=CD,
∴S1=S2;
(2)解:∵D是BC的中点,F是AD的中点,△ABC的面积12,
∴△ABD的面积=$\frac{1}{2}$△ABC的面积=6,△ABF的面积=$\frac{1}{2}$△ABD的面积=3;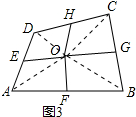
故答案为:3;
(3)解:如图3,连接OA、OB、OC、OD,
设△AOE的面积为m,
∵E、F、G、H分别是AD、AB、BC、CD边的中点,
∴△AOE的面积=△DOE的面积=m,△AOF的面积=△BOF的面积,△BOG的面积=△COG的面积,△DOH的面积=△COH的面积,
又∵四边形AFOE的面积为3,四边形BGOF的面积为5,四边形CHOG的面积4
∴△AOF的面积=△BOF的面积=3-m,
同理得:△BOG的面积=△COG的面积=5-(3-m)=2+m,△DOH的面积=△COH的面积=4-(2+m)=2-m,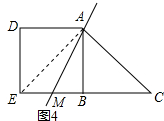
∴四边形DEOH的面积=△DOE的面积+△DOH的面积=m+2-m=2;
(4)解:连接AE,边长为2正方形ABED与边长为2等腰直角三角形ABC拼合在一起.
∴△ABC的面积=$\frac{1}{2}$正方形ABED的面积=△ABE的面积=△ADE的面积,
取BE的中点M,作直线AM,
则△ABM的面积=△AEM的面积,
∴△ACM的面积=四边形ADEM的面积,
即直线AM把四边形ADEC的面积分成相等的两部分,如图4所示.
点评 本题是三角形综合题目,考查了三角形的中线性质、正方形的性质、等腰直角三角形的性质等知识;本题综合性强,有一定难度,熟记三角形的中线把三角形面积分成相等的两部分是解决问题的关键.

 期末集结号系列答案
期末集结号系列答案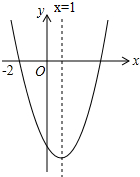 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b=0;③a+c>b;④抛物线与x轴的另一个交点为(3,0).其中正确的结论有( )个.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b=0;③a+c>b;④抛物线与x轴的另一个交点为(3,0).其中正确的结论有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | y=$\frac{2}{x}$ | B. | x-1=0 | C. | y=2(x-1) | D. | y=x2+1 |
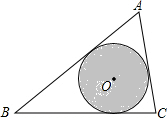 如图,△ABC中,AB=8,AC=5,∠A=60°,圆O是三角形的内切圆,如果在这个三角形内随意抛一粒豆子,则豆子落在圆O内的概率为$\frac{\sqrt{3}π}{10}$.
如图,△ABC中,AB=8,AC=5,∠A=60°,圆O是三角形的内切圆,如果在这个三角形内随意抛一粒豆子,则豆子落在圆O内的概率为$\frac{\sqrt{3}π}{10}$.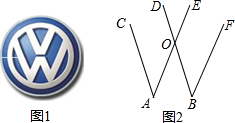 如图,图1是大众汽车的图标,图2反映其中直线间的关系,且AC∥BD,AE∥BF.
如图,图1是大众汽车的图标,图2反映其中直线间的关系,且AC∥BD,AE∥BF.
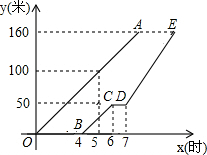 甲、乙两工程队维修同一段路面,甲队先清理路面,乙队在甲队清理后铺设路面.乙队在中途停工了一段时间,然后按停工前的工作效率继续工作.在整个工作过程中,甲队清理完的路面长y(米)与时间x(时)的函数图象为线段OA,乙队铺设完的路面长y(米)与时间x(时)的函数图象为折线BC--CD--DE,如图所示,从甲队开始工作时计时.
甲、乙两工程队维修同一段路面,甲队先清理路面,乙队在甲队清理后铺设路面.乙队在中途停工了一段时间,然后按停工前的工作效率继续工作.在整个工作过程中,甲队清理完的路面长y(米)与时间x(时)的函数图象为线段OA,乙队铺设完的路面长y(米)与时间x(时)的函数图象为折线BC--CD--DE,如图所示,从甲队开始工作时计时.