题目内容
10.若关于x的分式方程$\frac{2}{x-3}$+$\frac{x+m}{3-x}$=2有增根,则m的值为-1.分析 增根是分式方程化为整式方程后产生的使分式方程的分母为0的根.把增根代入化为整式方程的方程即可求出m的值.
解答 解:方程两边都乘(x-3),得
2-x-m=2(x-3)
∵原方程增根为x=3,
∴把x=3代入整式方程,得2-3-m=0,
解得m=-1.
故答案为:-1.
点评 考查了分式方程的增根,增根确定后可按如下步骤进行:①化分式方程为整式方程;②把增根代入整式方程即可求得相关字母的值.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
20.下列各式中一定是二次根式的是( )
| A. | $\sqrt{x}$ | B. | $\sqrt{{x}^{2}+1}$ | C. | $\sqrt{{x^2}-2}$ | D. | $\root{3}{27}$ |
1.一个正多边形的每个外角都是18°,这个正多边形的边数是( )
| A. | 9 | B. | 10 | C. | 19 | D. | 20 |
18.$\sqrt{2}$的相反数是( )
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
15. 如图,在△ABC纸片中,∠ABC=90°,将△ABC绕点B顺时针旋转90°,得到△A′BC′,连接CC′,若∠ACC′=15°,则∠A′的度数为( )
如图,在△ABC纸片中,∠ABC=90°,将△ABC绕点B顺时针旋转90°,得到△A′BC′,连接CC′,若∠ACC′=15°,则∠A′的度数为( )
 如图,在△ABC纸片中,∠ABC=90°,将△ABC绕点B顺时针旋转90°,得到△A′BC′,连接CC′,若∠ACC′=15°,则∠A′的度数为( )
如图,在△ABC纸片中,∠ABC=90°,将△ABC绕点B顺时针旋转90°,得到△A′BC′,连接CC′,若∠ACC′=15°,则∠A′的度数为( )| A. | 25° | B. | 30° | C. | 35° | D. | 40° |
19. 如图,平行四边形ABCD中,BD⊥AD,∠A=30°,BD=2,则CD的长为( )
如图,平行四边形ABCD中,BD⊥AD,∠A=30°,BD=2,则CD的长为( )
 如图,平行四边形ABCD中,BD⊥AD,∠A=30°,BD=2,则CD的长为( )
如图,平行四边形ABCD中,BD⊥AD,∠A=30°,BD=2,则CD的长为( )| A. | 1 | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
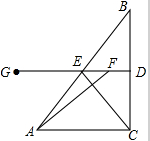 如图,在Rt△ABC中,∠ACB=90°,AC=4cm,动点F在线段BC的垂直平分线DG上,垂足为D,DG交AB于E,连接CE,AF,动点F从D点出发以1cm/s的速度移动,设运动时间为t(s).
如图,在Rt△ABC中,∠ACB=90°,AC=4cm,动点F在线段BC的垂直平分线DG上,垂足为D,DG交AB于E,连接CE,AF,动点F从D点出发以1cm/s的速度移动,设运动时间为t(s). 如图,四边形ABCD为正方形,点E、F在对角线BD上,点G在BC边上,EG⊥AE,GF⊥BD,若BF=3DE,CG=$\sqrt{2}$,则线段AE的长为5.
如图,四边形ABCD为正方形,点E、F在对角线BD上,点G在BC边上,EG⊥AE,GF⊥BD,若BF=3DE,CG=$\sqrt{2}$,则线段AE的长为5.