题目内容
因式分解：
（1）x2-4；
（2）x3-2x2+x．
（1）x2-4；
（2）x3-2x2+x．
考点：提公因式法与公式法的综合运用
专题：
分析：（1）直接利用平方差公式分解因式得出即可；
（2）首先提取公因式x，进而利用完全平方公式分解因式即可．
（2）首先提取公因式x，进而利用完全平方公式分解因式即可．
解答：解：（1）x2-4=（x+2）（x-2）；
（2）x3-2x2+x=x（x2-2x+1）=x（x-1）2．
（2）x3-2x2+x=x（x2-2x+1）=x（x-1）2．
点评：此题主要考查了提取公因式法以及公式法分解因式，熟练掌握乘法公式是解题关键．
练习册系列答案
科学实验活动册系列答案
相关题目
下列式子和说法中，正确的个数为（ ）
①
=±3；
②若m2=64，则m的立方根为2；
③
+1在连续整数4和5之间；
④
的平方根为±13；
⑤所有的有理数都可以在数轴上找到一个对应点，数轴上所有的点都表示有理数；
⑥两个有理数的和一定还是无理数；
⑦平方根等于本身的数只有0．
①
| (±3)2 |
②若m2=64，则m的立方根为2；
③
| 10 |
④
| 169 |
⑤所有的有理数都可以在数轴上找到一个对应点，数轴上所有的点都表示有理数；
⑥两个有理数的和一定还是无理数；
⑦平方根等于本身的数只有0．
| A、1个 | B、2个 | C、3个 | D、6个 |
下列各式中，属于最简二次根式的是（ ）
A、
| ||||
B、3x
| ||||
C、
| ||||
D、
|
已知二次函数的图象（0≤x≤3）如图，关于该函数在所给自变量取值范围内，下列说法正确的是（ ）| A、有最小值0，有最大值3 |
| B、有最小值0，有最大值4 |
| C、有最小值1，有最大值3 |
| D、无最小值，有最大值4 |
如图，在?ABCD中，AE⊥BC，AF⊥DC，垂足分别为E、F，∠ADC=60°，BE=4，CF=2．
在正方形网格中，每个小正方形的边长都为1个单位长度，△ABC的三个顶点的位置如图，现将△ABC平移后得△EDF，使点B的对应点为点D，点A对应点为点E．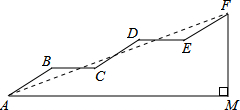
如图是某通道的侧面示意图，已知AB∥CD∥EF，AM∥BC∥DE，AB=CD=EF，∠AMF=90°，∠BAM=30°，AB=6m．