题目内容
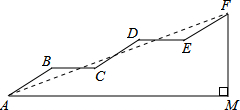 如图是某通道的侧面示意图,已知AB∥CD∥EF,AM∥BC∥DE,AB=CD=EF,∠AMF=90°,∠BAM=30°,AB=6m.
如图是某通道的侧面示意图,已知AB∥CD∥EF,AM∥BC∥DE,AB=CD=EF,∠AMF=90°,∠BAM=30°,AB=6m.(1)求FM的长;
(2)连接AF,若sin∠FAM=
| 1 |
| 3 |
考点:解直角三角形的应用-坡度坡角问题
专题:几何图形问题
分析:(1)分别过点B、D、F作BN⊥AM于点N,DG⊥BC延长线于点G,FH⊥DE延长线于点H,根据AB∥CD∥EF,AM∥BC∥DE,分别解Rt△ABN、Rt△DCG、Rt△FEH,求出BN、DG、FH的长度,继而可求出FM的长度;
(2)在Rt△FAM中,根据sin∠FAM=
,求出AF的长度,然后利用勾股定理求出AM的长度.
(2)在Rt△FAM中,根据sin∠FAM=
| 1 |
| 3 |
解答:解: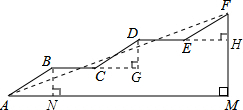 (1)分别过点B、D、F作BN⊥AM于点N,DG⊥BC延长线于点G,FH⊥DE延长线于点H,
(1)分别过点B、D、F作BN⊥AM于点N,DG⊥BC延长线于点G,FH⊥DE延长线于点H,
在Rt△ABN中,
∵AB=6m,∠BAM=30°,
∴BN=ABsin∠BAN=6×
=3m,
∵AB∥CD∥EF,AM∥BC∥DE,
同理可得:DG=FH=3m,
∴FM=FH+DG+BN=9m;
(2)在Rt△FAM中,
∵FM=9m,sin∠FAM=
,
∴AF=27m,
∴AM=
=18
(m).
即AM的长为18
m.
 (1)分别过点B、D、F作BN⊥AM于点N,DG⊥BC延长线于点G,FH⊥DE延长线于点H,
(1)分别过点B、D、F作BN⊥AM于点N,DG⊥BC延长线于点G,FH⊥DE延长线于点H,在Rt△ABN中,
∵AB=6m,∠BAM=30°,
∴BN=ABsin∠BAN=6×
| 1 |
| 2 |
∵AB∥CD∥EF,AM∥BC∥DE,
同理可得:DG=FH=3m,
∴FM=FH+DG+BN=9m;
(2)在Rt△FAM中,
∵FM=9m,sin∠FAM=
| 1 |
| 3 |
∴AF=27m,
∴AM=
| AF2-FM2 |
| 2 |
即AM的长为18
| 2 |
点评:本题考查了解直角三角形的应用,解答本题的关键是根据坡角构造直角三角形,利用三角函数解直角三角形,注意勾股定理的应用.

练习册系列答案
相关题目
代数式的家中来了几位客人:
、
、
、
、
,其中属于分式家族成员的有( )
| 2 |
| x |
| x+y |
| 5 |
| 1 |
| 2-a |
| x |
| π-1 |
| x |
| 2x+1 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图是两个全等的含30°角的直角三角形.
如图是两个全等的含30°角的直角三角形.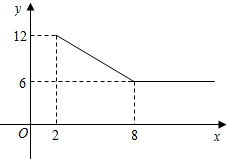 某公司经营杨梅业务,以3万元/吨的价格向农户收购杨梅后,分拣成A、B两类,A类杨梅包装后直接销售;B类杨梅深加工后再销售.A类杨梅的包装成本为1万元/吨,根据市场调查,它的平均销售价格y(单位:万元/吨)与销售数量x(x≥2)之间的函数关系如图;B类杨梅深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.
某公司经营杨梅业务,以3万元/吨的价格向农户收购杨梅后,分拣成A、B两类,A类杨梅包装后直接销售;B类杨梅深加工后再销售.A类杨梅的包装成本为1万元/吨,根据市场调查,它的平均销售价格y(单位:万元/吨)与销售数量x(x≥2)之间的函数关系如图;B类杨梅深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨. 电脑中有一种游戏--蜘蛛纸牌,开始游戏前有500分的基本分,游戏规则如下:
电脑中有一种游戏--蜘蛛纸牌,开始游戏前有500分的基本分,游戏规则如下: