题目内容
如图，在?ABCD中，AE⊥BC，AF⊥DC，垂足分别为E、F，∠ADC=60°，BE=4，CF=2．（1）从对称性质看，?ABCD是
（2）求平行四边形ABCD的周长．
考点：平行四边形的性质,中心对称图形
专题：
分析：（1）根据平行四边形的性质可知：对角线互相平分，所以O为旋转中心，即平行四边形ABCD是中心对称图形；
（2）根据平行四边形中对角、对边分别相等，∠B=∠ADC=60°，再根据已知边长，由勾股定理可求出AB、AD的长，进而可求出平行四边形ABCD的周长．
（2）根据平行四边形中对角、对边分别相等，∠B=∠ADC=60°，再根据已知边长，由勾股定理可求出AB、AD的长，进而可求出平行四边形ABCD的周长．
解答：解：（1）∵四边形ABCD是平行四边形，
∴对角线互相平分，
∴O为旋转中心，
即平行四边形ABCD是中心对称图形，
故答案为：中心；
（2）∵四边形ABCD是平行四边形，
∴∠B=∠D=60°，AB=CD，AD=BC．
∵AE⊥BC，
∵BE=4，
∴AB=8，
∴CD=AB=8，
∵CF=2，∴DF=6，
∵AF⊥DC，∠D=60°
∴在Rt△ADF中，AD=12，
∴平行四边形ABCD的周长=2（12+8）=40．
∴对角线互相平分，
∴O为旋转中心，
即平行四边形ABCD是中心对称图形，
故答案为：中心；
（2）∵四边形ABCD是平行四边形，
∴∠B=∠D=60°，AB=CD，AD=BC．
∵AE⊥BC，
∵BE=4，
∴AB=8，
∴CD=AB=8，
∵CF=2，∴DF=6，
∵AF⊥DC，∠D=60°
∴在Rt△ADF中，AD=12，
∴平行四边形ABCD的周长=2（12+8）=40．
点评：本题考查了平行四边形的性质，运用平行四边形的性质解决以下问题，如求角的度数、线段的长度，证明角相等或互补，证明线段相等或倍分等．
练习册系列答案
53随堂测系列答案
相关题目
某加油站九月份营销某种油品的销售利润y（万元）与销售量 x（万升）之间的函数图象如图中折线所示，该加油站截止到13日调价时的销售利润为4万元，截止至15日进油时的销售利润为5.5万元．（销售利润=（售价-成本价）×销售量）．请你根据图象及加油站五月份该油品的所有销售记录提供的信息，解答：求线段BC所对应的函数关系式，写出自变量的取值范围（ ）
| A、y=1.5x-2，4≤x≤5 |
| B、y=1.1x，5≤x≤10 |
| C、y=1.1x，4≤x≤10 |
| D、y=1.5x-2，4≤x≤10 |
已知M（2，-3），N（-2，-3），则直线MN与x轴和y轴的位置关系分别为（ ）
| A、垂直、垂直 |
| B、平行、平行 |
| C、垂直、平行 |
| D、平行、垂直 |
如图是两个全等的含30°角的直角三角形．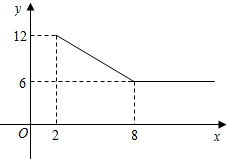
某公司经营杨梅业务，以3万元/吨的价格向农户收购杨梅后，分拣成A、B两类，A类杨梅包装后直接销售；B类杨梅深加工后再销售．A类杨梅的包装成本为1万元/吨，根据市场调查，它的平均销售价格y（单位：万元/吨）与销售数量x（x≥2）之间的函数关系如图；B类杨梅深加工总费用s（单位：万元）与加工数量t（单位：吨）之间的函数关系是s=12+3t，平均销售价格为9万元/吨．