题目内容
 如图所示,正方形ABCD中,E、F分别是AB和AD上的点,若CE⊥BF于点M,
如图所示,正方形ABCD中,E、F分别是AB和AD上的点,若CE⊥BF于点M,求证:AF=BE.
考点:正方形的性质,全等三角形的判定与性质
专题:证明题
分析:首先证明利用等角的余角相等得出∠ECB=∠ABF,再证明△ABF≌△BCE即可得到BE=AF;
解答:证明:∵四边形ABCD是正方形,
∴AB=BC,∠A=∠ABC=90°,
∴∠CBM+∠ABF=90°,
∵CE⊥BF,
∴∠ECB+∠MBC=90°,
∴∠ECB=∠ABF,
在△ABF和△BCE中,
,
∴△ABF≌△BCE(ASA),
∴BE=AF.
∴AB=BC,∠A=∠ABC=90°,
∴∠CBM+∠ABF=90°,
∵CE⊥BF,
∴∠ECB+∠MBC=90°,
∴∠ECB=∠ABF,
在△ABF和△BCE中,
|
∴△ABF≌△BCE(ASA),
∴BE=AF.
点评:此题主要考查了全等三角形的判定与性质,以及正方形的性质,关键是掌握全等三角形的判定方法.

练习册系列答案
相关题目
如图,∠1与∠2互为邻补角的是( )
A、 |
B、 |
C、 |
D、 |
 如图所示,已知BE平分∠ABC,CF平分∠BCD,图中内错角有多少对?
如图所示,已知BE平分∠ABC,CF平分∠BCD,图中内错角有多少对?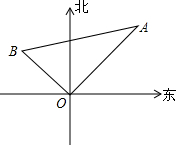 一艘轮船以16海里/时的速度离开港口(如图),向北偏东40°方向航行,另一艘轮船在同时以12海里/时的速度向北偏西一定的角度的航向行驶,已知它们离港口一个半小时后相距30海里(即BA=30),问另一艘轮船的航行的方向是北偏西多少度?
一艘轮船以16海里/时的速度离开港口(如图),向北偏东40°方向航行,另一艘轮船在同时以12海里/时的速度向北偏西一定的角度的航向行驶,已知它们离港口一个半小时后相距30海里(即BA=30),问另一艘轮船的航行的方向是北偏西多少度?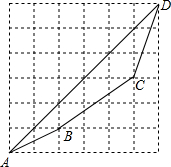 比较两个实数大小的方法很多,用构造法来比较大小,体现了数形结合的思想,别具一格.例如比较
比较两个实数大小的方法很多,用构造法来比较大小,体现了数形结合的思想,别具一格.例如比较 如图所示
如图所示