题目内容
如图所示，AD是△ABC的高，AB=10，AD=8，BC=12，求证：△ABC是等腰三角形．考点：勾股定理的逆定理,等腰三角形的判定
专题：证明题
分析：在Rt△ABD中，先由勾股定理得到BD的长，进一步得到CD的长，在Rt△ACD中，再根据勾股定理得到AC的长，从而证明△ABC是等腰三角形．
解答：证明：∵AD是△ABC的高，
∴△ABD，△ACD是直角三角形，
在Rt△ABD中，AB=10，AD=8，
∴BD=6，
∵BC=12，
∴CD=6，
在Rt△ACD中，AC=10，
AB=AC，
∴△ABC是等腰三角形．
∴△ABD，△ACD是直角三角形，
在Rt△ABD中，AB=10，AD=8，
∴BD=6，
∵BC=12，
∴CD=6，
在Rt△ACD中，AC=10，
AB=AC，
∴△ABC是等腰三角形．
点评：考查了勾股定理和等腰三角形的判定，本题关键是根据勾股定理得到BD的长，进一步得到CD的长．
练习册系列答案
相关题目
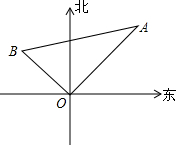一艘轮船以16海里/时的速度离开港口（如图），向北偏东40°方向航行，另一艘轮船在同时以12海里/时的速度向北偏西一定的角度的航向行驶，已知它们离港口一个半小时后相距30海里（即BA=30），问另一艘轮船的航行的方向是北偏西多少度？
如图所示，已知∠1=110°，∠3=110°，∠4=70°
如图所示
如图所示
已知三角形ABC的两个顶点坐标为A（-4，0），B（2，0），如图，且过这两个点的边上的高为4，第三个顶点的横坐标为-1，求顶点C的坐标及三角形的面积．
如图，在平行四边形ABCD中，E，F，G，H分别是边AB，BC，CD，DA上的点，且AE=CG，BF=DH，求证：EG与FH互相平分（提示：可连接EF，FG，GH，HE，证四边形EFGH为平行四边形即可）．
如图所示，把一根筷子一端放在水里，一端露出水面，筷子变弯了，它真的弯了吗？其实没有，这是光的折射现象，光从空气中射入水中，光的传播方向发生了改变．