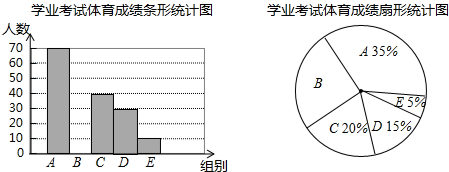
题目内容
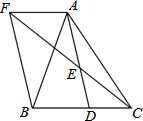 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BF的平行线,交CE的延长线于点F,且AF=BD,连接BF.如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BF的平行线,交CE的延长线于点F,且AF=BD,连接BF.如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.考点:矩形的判定,全等三角形的判定与性质
专题:
分析:因为AF∥BC,E为AD的中点,即可根据AAS证明△AEF≌△DEC,故有BD=DC,AF=DC且AF∥DC,可得四边形AFDC是平行四边形,又因为AD=CF,故可有一个角是直角的平行四边形是矩形进行判定.
解答:答:四边形AFBD是矩形,
证明:∵AF∥BC,
∴∠AFE=∠DCE,∠FAE=∠CDE.
又∵点E是AD的中点,
∴AE=DE,
在△AFE与△DCE中,
∴△AFE≌△DCE(AAS),
∴AF=CD,
又∵AF=BD,
∴BD=CD.
又∵AB=AC,
∴AD⊥BC,
∴∠ADB=90°,
∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
又∵∠ADB=90°,
∴四边形AFBD是矩形.
证明:∵AF∥BC,
∴∠AFE=∠DCE,∠FAE=∠CDE.
又∵点E是AD的中点,
∴AE=DE,
在△AFE与△DCE中,
|
∴△AFE≌△DCE(AAS),
∴AF=CD,
又∵AF=BD,
∴BD=CD.
又∵AB=AC,
∴AD⊥BC,
∴∠ADB=90°,
∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
又∵∠ADB=90°,
∴四边形AFBD是矩形.
点评:本题考查矩形的判定和全等三角形的判定与性质.要熟知这些判定定理才会灵活运用,根据性质才能得到需要的相等关系.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
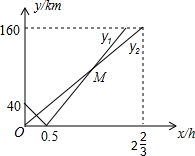 某次海军舰艇演习中,甲、乙两舰艇同时从A、B两个港口出发,均沿直线匀速驶向演习目标地海岛C,两舰艇都到达C岛后演习第一阶段结束.已知B港位于A港、C岛之间,且A、B、C在一条直线上.设甲、乙两舰艇行驶x(h)后,与B港的距离分别为y1和y2(km),y1、y2与x的函数关系如图所示.
某次海军舰艇演习中,甲、乙两舰艇同时从A、B两个港口出发,均沿直线匀速驶向演习目标地海岛C,两舰艇都到达C岛后演习第一阶段结束.已知B港位于A港、C岛之间,且A、B、C在一条直线上.设甲、乙两舰艇行驶x(h)后,与B港的距离分别为y1和y2(km),y1、y2与x的函数关系如图所示.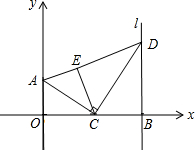 如图,点A的坐标是(0,2),点B是x轴正半轴上的点,过点B作直线l垂直于x轴,点C为线段OB上的动点,连接AC,过点C作CD⊥AC交直线l于点D,将△BCD沿CD翻折至△ECD的位置,连接AE,设点B的坐标是(m,0),点C的坐标是(n,0)
如图,点A的坐标是(0,2),点B是x轴正半轴上的点,过点B作直线l垂直于x轴,点C为线段OB上的动点,连接AC,过点C作CD⊥AC交直线l于点D,将△BCD沿CD翻折至△ECD的位置,连接AE,设点B的坐标是(m,0),点C的坐标是(n,0)
 抛物线y=x2-kx-3与x轴交于点A,B,与y轴交于点C,其中点B的坐标为(1+k,0).
抛物线y=x2-kx-3与x轴交于点A,B,与y轴交于点C,其中点B的坐标为(1+k,0).