题目内容
13.如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA、AO,并延长AO交⊙O于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若$\frac{OC}{AC}$=$\frac{2}{3}$,且OC=4,求PA的长.
分析 (1)证明△PAO≌△PBO可得结论;
(2)根据∠POA的余切列式,可以求出PA的长.
解答 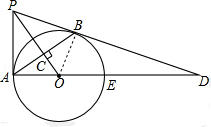 (1)证明:连接OB,
(1)证明:连接OB,
∵PB为⊙O的切线,
∴OB⊥PB,
∴∠PBO=90°,
∵OP⊥AB,
∴AC=BC,
∴OP是AB的垂直平分线,
∴PA=PB,
∵OA=OB,PO=PO,
∴△PAO≌△PBO,
∴∠PAO=∠PBO=90°,
∴PA⊥OA,
∴PA是⊙O的切线;
(2)∵$\frac{OC}{AC}$=$\frac{2}{3}$,且OC=4,
∴AC=6,
∴AO=$\sqrt{{4}^{2}+{6}^{2}}$=$\sqrt{16+36}$=2$\sqrt{13}$,
在Rt△PAO中,∵AB⊥PO,
∴tan∠POA=$\frac{AC}{OC}=\frac{PA}{AO}$,
∴$\frac{3}{2}=\frac{PA}{2\sqrt{3}}$,
∴PA=3$\sqrt{13}$.
点评 本题考查了切线的性质和判定,做好本题是明确两点:①圆的切线垂直于经过切点的半径. ②经过半径的外端且垂直于这条半径的直线是圆的切线;要利用比例式计算边的长度时,利用三角函数列式比相似要简单些.

练习册系列答案
相关题目
7.下列说法错误的是( )
| A. | 在正多边形中,只有正三角形、正四边形、正六边形可以铺满地板 | |
| B. | 任意的三角形、任意的四边形都可以铺满地板 | |
| C. | 每个内角都相等的多边形就是正多边形 | |
| D. | 每条边都相等的多边形不一定是正多边形 |
8.下列图形中,是轴对称图形并且对称轴条数最多的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在△ABC中,∠C=90°,AC=4,BC=3,以点C为圆心,r为半径画圆.
如图,在△ABC中,∠C=90°,AC=4,BC=3,以点C为圆心,r为半径画圆. 如图,在平面直角坐标系xOy中,菱形MNPQ的顶点P的坐标为(2,0),点N的坐标为(0,1),点M在第一象限,对角线NQ与x轴平行,直线y=x+8与x轴、y轴分别交于点A、B,将菱形MNPQ沿x轴向左平移k个单位,当点M落在△AOB内部时(不包括三角形的边),下列数据中不可能为k的值的是( )
如图,在平面直角坐标系xOy中,菱形MNPQ的顶点P的坐标为(2,0),点N的坐标为(0,1),点M在第一象限,对角线NQ与x轴平行,直线y=x+8与x轴、y轴分别交于点A、B,将菱形MNPQ沿x轴向左平移k个单位,当点M落在△AOB内部时(不包括三角形的边),下列数据中不可能为k的值的是( ) 如图,一次函数y=kx+b(k≠0)的图象过点P(-$\frac{3}{2}$,0)且与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A(2,1)和点B.
如图,一次函数y=kx+b(k≠0)的图象过点P(-$\frac{3}{2}$,0)且与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A(2,1)和点B. 如图,反比例函数y=$\frac{k}{x}$的图象与矩形AOBC的边AC交于E,且AE=2CE,与另一边BC交于点D,连接DE,若S△CED=1,则k的值为12.
如图,反比例函数y=$\frac{k}{x}$的图象与矩形AOBC的边AC交于E,且AE=2CE,与另一边BC交于点D,连接DE,若S△CED=1,则k的值为12. △ABC是等腰直角三角形,∠BAC=90°,D是BC的中点,CE⊥AE,若DE=8$\sqrt{2}$,AE=3EC,求:BE的长.
△ABC是等腰直角三角形,∠BAC=90°,D是BC的中点,CE⊥AE,若DE=8$\sqrt{2}$,AE=3EC,求:BE的长.