Question

8．如图，在△ABC中，∠C=90°，AC=4，BC=3，以点C为圆心，r为半径画圆．
（1）当r=2.4时，⊙C与边AB相切；
（2）当r满足3＜r≤4或r=2.4时，⊙C与边AB只有一个交点；
（3）随着r的变化，⊙C与边AB的交点个数还有哪些变化？写出相应的r的值或取值范围．

Answer 1

分析 （1）当⊙C与边AB相切时，则d=r，由此求出r的值即可；
（2）根据直线与圆的位置关系得出相切时有一交点，再结合图形得出另一种有一个交点的情况，即可得出答案；
（3）随着r的变化，⊙C与边AB的交点个数由0个、1个、2个三种情况．

解答 解：（1）过点C作CD⊥AB于点D，
∵AC=3，BC=4．如果以点C为圆心，r为半径的圆与斜边AB只有一个公共点，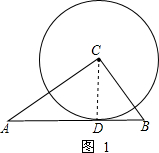
∴AB=5，
当直线与圆相切时，d=r，圆与斜边AB只有一个公共点，圆与斜边AB只有一个公共点，如图1，
∴CD×AB=AC×BC，
∴CD=r=2.4，
故答案为：r=2.4．
（2）①当直线与圆相切时，即d=r=2.4，圆与斜边AB只有一个公共点，圆与斜边AB只有一个公共点，
②当直线与圆如图所示也可以有一个交点，如图2，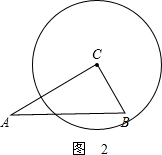
∴3＜r≤4，
故答案为：3＜r≤4或r=2.4；
（3）①如图3，当0≤r＜2.4时，圆C与边AB有0个交点；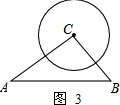
②如图1，当r=2.4时，圆C与边AB有1个交点；
③如图4，当2.4＜r≤3时，圆C与边AB有2个交点；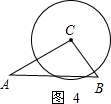
④如图2，当3＜r≤4时，圆C与边AB有1个交点；
⑤如图5，当r＞4时，圆C与边AB有0个交点；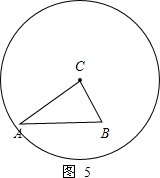
综上所述，当0≤r＜2.4或r＞4时，圆C与边AB有0个交点；
当3＜r≤4或r=2.4时，圆C与边AB有1个交点；
当2.4＜r≤3时，圆C与边AB有2个交点．

点评 本题主要考查圆与直线的位置关系，明确随r的变化，圆C与边AB的交点个数也是不同的，能根据交点的不同明确r的取值范围是解决此题的关键．