题目内容
12. 如图,已知点A,B,C,D均在⊙O上,CD为∠ACE的角平分线.
如图,已知点A,B,C,D均在⊙O上,CD为∠ACE的角平分线.(1)求证:△ABD为等腰三角形;
(2)若∠DCE=45°,BD=6,求⊙O的半径.
分析 (1)欲证明△ABD为等腰三角形,只要证明∠DBA=∠DAB即可.
(2)如图2中,只要证明AB是直径即可解决问题.
解答 解:(1)如图1中,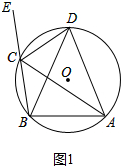
∵CD平分∠EAC,
∴∠ECD=∠DCA,
∵∠ECD=∠DAB,∠DCA=∠DBA,
∴∠DBA=∠DAB,
∴DB=DA.
∵△DBA是等腰三角形.
(2)如图2中,
∵∠DCE=∠DCA=45°,
∴∠ECA=∠ACB=90°,
∴AB是直径,
∴∠BDA=90°,
∵BD=AD=6,
∴AB=$\sqrt{B{D}^{2}+D{A}^{2}}$=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$.
∴⊙O的半径为3$\sqrt{2}$
点评 本题考查圆周角、圆内接四边形的性质、等腰三角形的判定、直角三角形的判定、勾股定理等知识,解题的关键是灵活应用这些知识解决问题,属于基础题,中考常考题型.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
4. 如图,已知长方体ABCD-EFGH,那么下列直线中与直线BC异面的是( )
如图,已知长方体ABCD-EFGH,那么下列直线中与直线BC异面的是( )
 如图,已知长方体ABCD-EFGH,那么下列直线中与直线BC异面的是( )
如图,已知长方体ABCD-EFGH,那么下列直线中与直线BC异面的是( )| A. | EF | B. | AD | C. | CG | D. | EH |
 如图,在正方形ABCD中,对角线AC、BD相交于点O,∠BAC的平分线交BD于点G,交BC于点E,过点A作AF⊥AE交CD的延长线于点F,连接EF交BD于点M,若OG+CE=2$\sqrt{7}$,则DM的长为$\frac{2\sqrt{14}}{3}$.
如图,在正方形ABCD中,对角线AC、BD相交于点O,∠BAC的平分线交BD于点G,交BC于点E,过点A作AF⊥AE交CD的延长线于点F,连接EF交BD于点M,若OG+CE=2$\sqrt{7}$,则DM的长为$\frac{2\sqrt{14}}{3}$.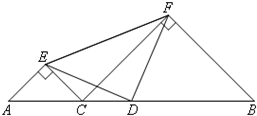 已知:如图,D为线段AB的中点,在AB上任取一点C(不与点A,B,D重合),分别以AC,BC为斜边在AB同侧作等腰Rt△ACE与等腰Rt△BCF,∠AEC=∠CFB=90°,连接DE,DF,EF.
已知:如图,D为线段AB的中点,在AB上任取一点C(不与点A,B,D重合),分别以AC,BC为斜边在AB同侧作等腰Rt△ACE与等腰Rt△BCF,∠AEC=∠CFB=90°,连接DE,DF,EF. 如图,长方形ABCD是由k个相同的长方形组成,上下各有4个水平放置的长方形,中间竖放若干个长方形,并且宽AB是长AD的$\frac{7}{12}$,则k的值为14.
如图,长方形ABCD是由k个相同的长方形组成,上下各有4个水平放置的长方形,中间竖放若干个长方形,并且宽AB是长AD的$\frac{7}{12}$,则k的值为14. 如图,两张48×40的长方形纸片有一个顶点重合,重叠放置的尺寸如图所标示,则图中阴影部分的面积=984.
如图,两张48×40的长方形纸片有一个顶点重合,重叠放置的尺寸如图所标示,则图中阴影部分的面积=984.