题目内容
15.(1)计算:(π-2017)0-$\frac{\sqrt{8}}{2}$+(sin45°)-1-|tan60°-$\sqrt{12}$|(2)解方程:(x-1)(x-3)=6.
分析 (1)将特殊角的三角函数值代入,再根据实数的混合运算顺序和法则计算可得;
(2)整理成一般式后,公式法求解可得.
解答 解:(1)原式=1-$\sqrt{2}$+$\sqrt{2}$-|$\sqrt{3}$-2$\sqrt{3}$|
=1-$\sqrt{3}$;
(2)原式变为x2-4x-3=0,
∵a=1,b=-4,c=-3,
∴△=16-4×1×(-3)=28>0,
则x=$\frac{4±2\sqrt{7}}{2}$=2$±\sqrt{7}$,
∴x1=2+$\sqrt{7}$,x2=2-$\sqrt{7}$.
点评 本题主要考查特殊角的三角函数值、实数的混合运算及解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
相关题目
5.滕州市某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
经统计发现两班总数相等,此时有学生建议,可以通过考察数据中的其他信息作为参考,请你回答下列问题:
(1)分别求出两班5名学生比赛成绩的中位数;
(2)计算并比较两班比赛数据的方差哪个小?
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
| 1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
| 甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
| 乙班 | 100 | 95 | 110 | 91 | 104 | 500 |
(1)分别求出两班5名学生比赛成绩的中位数;
(2)计算并比较两班比赛数据的方差哪个小?
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
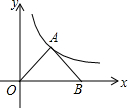 已知,如图所示,在平面直角坐标系中,Rt△OAB的直角顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,∠AOB=30°,顶点B在x轴上,求此△OAB顶点A的坐标和△OAB面积.
已知,如图所示,在平面直角坐标系中,Rt△OAB的直角顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,∠AOB=30°,顶点B在x轴上,求此△OAB顶点A的坐标和△OAB面积.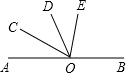 如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=α,求∠BOE的度数.
如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=α,求∠BOE的度数. 如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A、C两点,与x轴的另一交点为点B,连结BC.
如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A、C两点,与x轴的另一交点为点B,连结BC.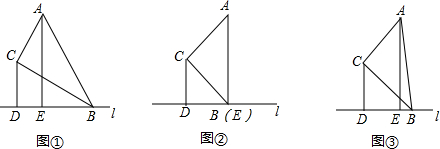
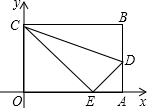 如图,平面直角坐标系中,四边形OABC是长方形,O为原点,点A在x轴上,点C在y轴上且A(10,0),C(0,6),点D在AB边上,将△CBD沿CD翻折,点B恰好落在OA边上点E处.
如图,平面直角坐标系中,四边形OABC是长方形,O为原点,点A在x轴上,点C在y轴上且A(10,0),C(0,6),点D在AB边上,将△CBD沿CD翻折,点B恰好落在OA边上点E处.