题目内容
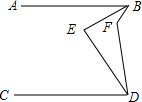 如图,AB∥CD,BE平分∠ABF,DE平分∠CDF,∠BFD=120°,求∠BED.
如图,AB∥CD,BE平分∠ABF,DE平分∠CDF,∠BFD=120°,求∠BED.考点:平行线的性质
专题:计算题
分析:连接BD,过F作FG∥AB,由AB∥CD,得到FG∥CD,利用两直线平行内错角相等,得到两对角相等,进而求出∠ABF+∠CDF的度数,由BE平分∠ABF,DE平分∠CDF,利用角平分线定义得到∠EBF+∠EFF的度数,在三角形BFD中,利用内角和定理得到∠FBD+∠FDB的度数,进而求出∠EBD+∠EDB的度数,求出∠BED度数即可.
解答: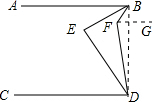 解:连接BD,过F作FG∥AB,由AB∥CD,得到FG∥CD,
解:连接BD,过F作FG∥AB,由AB∥CD,得到FG∥CD,
∴∠ABF=∠BFG,∠CDF=∠DFG,
∴∠BFD=∠ABF+∠CDF=120°,∠FBD+∠FDB=60°,
∵BE平分∠ABF,DE平分∠CDF,
∴∠EBF+∠EDF=
(∠ABF+∠CDF)=60°,
∴∠EBD+∠EDB=∠EBF+∠EDF+∠FBD+∠FDB=120°,
则∠BED=60°.
 解:连接BD,过F作FG∥AB,由AB∥CD,得到FG∥CD,
解:连接BD,过F作FG∥AB,由AB∥CD,得到FG∥CD,∴∠ABF=∠BFG,∠CDF=∠DFG,
∴∠BFD=∠ABF+∠CDF=120°,∠FBD+∠FDB=60°,
∵BE平分∠ABF,DE平分∠CDF,
∴∠EBF+∠EDF=
| 1 |
| 2 |
∴∠EBD+∠EDB=∠EBF+∠EDF+∠FBD+∠FDB=120°,
则∠BED=60°.
点评:此题考查了平行线的性质,角平分线定义,熟练掌握平行线的性质是解本题的关键.

练习册系列答案
相关题目
如果-
a2b2n-1是五次单项式,则n的值为( )
| π |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
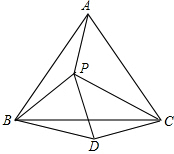 已知:如图,点P是等边△ABC内的一点,连结PA,PB,PC,以BP为边作等边△BPD,连结CD.
已知:如图,点P是等边△ABC内的一点,连结PA,PB,PC,以BP为边作等边△BPD,连结CD. 如图,为了测量山坡的护坡石坝与地面的倾斜角α,把一根长为4.5m的竹竿AC斜靠在石坝旁,量出竿长1米时它离地面的高度为0.6m,又量得竿顶与坝脚的距离BC=2.8m,这样∠α就可以计算出来了,请你算一算.
如图,为了测量山坡的护坡石坝与地面的倾斜角α,把一根长为4.5m的竹竿AC斜靠在石坝旁,量出竿长1米时它离地面的高度为0.6m,又量得竿顶与坝脚的距离BC=2.8m,这样∠α就可以计算出来了,请你算一算.