题目内容
5. 如图,已知梯形ABCD中,AB∥DC,△AOB的面积等于9平方厘米,△AOD的面积等于6平方厘米.
如图,已知梯形ABCD中,AB∥DC,△AOB的面积等于9平方厘米,△AOD的面积等于6平方厘米.(1)求△BOC的面积;
(2)求$\frac{DO}{OB}$和$\frac{CO}{OA}$的值.
分析 (1)根据等高不同底的两三角形面积的比等于底的比得到$\frac{OD}{OB}$=$\frac{{S}_{△AOD}}{{S}_{△AOB}}$=$\frac{6}{9}$=$\frac{2}{3}$,由于AB∥DC,得到△COD∽△ABO,根据相似三角形的性质即可得到结论;
(2)由(1)证得$\frac{DO}{OB}$=$\frac{CO}{OA}$=$\frac{2}{3}$,结论可得.
解答 解:(1)∵△AOB的面积等于9平方厘米,△AOD的面积等于6平方厘米.
∴$\frac{OD}{OB}$=$\frac{{S}_{△AOD}}{{S}_{△AOB}}$=$\frac{6}{9}$=$\frac{2}{3}$,
∵AB∥DC,
∴△COD∽△ABO,
∴$\frac{OC}{OA}=\frac{OD}{OB}$=$\frac{2}{3}$,
∴$\frac{{S}_{△BOC}}{{S}_{△AOB}}$=$\frac{OC}{OA}$=$\frac{2}{3}$,
∴△BOC的面积=4;
(2)由(1)证得$\frac{DO}{OB}$=$\frac{CO}{OA}$=$\frac{2}{3}$,
∴$\frac{DO}{OB}$和$\frac{CO}{OA}$的值都为$\frac{2}{3}$.
点评 本题考查了相似三角形的判定和性质,三角形的面积,知道等高不同底的两三角形面积的比等于底的比是解题的关键.

练习册系列答案
相关题目
15.已知方程2x2-x-3=0的两根为x1,x2,那么$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | 3 | D. | -3 |
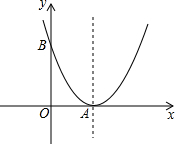 如图,以A为顶点的抛物线与y轴交于点B,已知A,B两点的坐标分别为(3,0)、(0,4).
如图,以A为顶点的抛物线与y轴交于点B,已知A,B两点的坐标分别为(3,0)、(0,4).