题目内容
20.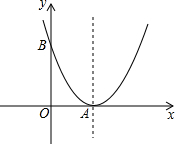 如图,以A为顶点的抛物线与y轴交于点B,已知A,B两点的坐标分别为(3,0)、(0,4).
如图,以A为顶点的抛物线与y轴交于点B,已知A,B两点的坐标分别为(3,0)、(0,4).(1)求此抛物线的解析式;
(2)将y轴向右平移6个单位长度,写出此时抛物线的解析式;
(3)抛物线上是否存在一点P,使AB=AP?若存在,请求出点P的坐标;若不存在,请说明理由.
分析 (1)已知抛物线的顶点坐标,所以设抛物线解析式为顶点式:y=a(x-3)2,然后把点B的坐标代入进行求值即可;
(2)根据题意求得平移后抛物线的顶点坐标,然后写出平移后抛物线的解析式;
(3)设P(x、y)利用两点间的距离公式得到关于y的方程,通过解方程求得y的值,进而由抛物线上点的坐标特征得到点P的横坐标.
解答 解:(1)设抛物线解析式为:y=a(x-3)2,(a≠0),
把点B的坐标(0,4)代入,得
4=a(0-3)2,
解得a=$\frac{4}{9}$.
所以该抛物线的解析式为:y=$\frac{4}{9}$(x-3)2;
(2)将y轴向右平移6个单位长度后该抛物线的顶点坐标为(-3,0),
则平移后抛物线的解析式为:y=$\frac{4}{9}$(x+3)2;
(3)设P(x、y),
∵AB=AP,A(3,0)、B(0,4),
∴AB2=AP2,即32+42=(x-3)2+y2,
∴25=$\frac{9}{4}$y+y2,即(y-4)(4y+25)=0,
解得y=4或y=-$\frac{25}{4}$(舍去),
则4=$\frac{4}{9}$(x-3)2,
解得x=6或x=0(舍去).
综上所述,点P的坐标是(6,4).
点评 本题考查了二次函数图象的几何变换,二次函数图象上点的坐标特征以及待定系数法求二次函数解析式.解答(3)题时,也可以利用抛物线的对称性直接得到点P的纵坐标,然后由二次函数图象上点的坐标特征来求点P的横坐标.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
11.任意抛掷一枚均匀的骰子,结果朝上一面的点数为偶数的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
 如图,在一个三角形点阵中,从上向下数有无数多行,其中各行点数依次为2,4,6,…,2n,请你探究出前n行的点数所满足的规律.若前n行点数和为420则n为( )
如图,在一个三角形点阵中,从上向下数有无数多行,其中各行点数依次为2,4,6,…,2n,请你探究出前n行的点数所满足的规律.若前n行点数和为420则n为( ) 如图,已知梯形ABCD中,AB∥DC,△AOB的面积等于9平方厘米,△AOD的面积等于6平方厘米.
如图,已知梯形ABCD中,AB∥DC,△AOB的面积等于9平方厘米,△AOD的面积等于6平方厘米.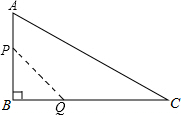 如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,设运动的时间为x s,四边形APQC的面积为y mm2.
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,设运动的时间为x s,四边形APQC的面积为y mm2. 如图,∠B=∠C,D在BC上,∠BAD=30°,在AC上取AE=AD,∠ADE=∠AED,求∠EDC的度数.
如图,∠B=∠C,D在BC上,∠BAD=30°,在AC上取AE=AD,∠ADE=∠AED,求∠EDC的度数.