题目内容
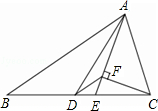 如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,求DF的长.
如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,求DF的长.考点:三角形中位线定理,等腰三角形的判定与性质
专题:
分析:延长CF交AB于H,根据等腰三角形三线合一的性质可得CF=FH,AH=AC,然后求出BH,再根据三角形的中位线平行于第三边并且等于第三边的一半可得DF=
BH.
| 1 |
| 2 |
解答: 解:如图,延长CF交AB于H,
解:如图,延长CF交AB于H,
∵AE是角平分线,CF⊥AE,
∴CF=FH,AH=AC,
∴BH=AB-AH=AB-AC=5-2=3,
又∵AD是中线,
∴DF是△BCH的中位线,
∴DF=
BH=
×3=1.5.
 解:如图,延长CF交AB于H,
解:如图,延长CF交AB于H,∵AE是角平分线,CF⊥AE,
∴CF=FH,AH=AC,
∴BH=AB-AH=AB-AC=5-2=3,
又∵AD是中线,
∴DF是△BCH的中位线,
∴DF=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,等腰三角形三线合一的性质,作辅助线构造出以DF为中位线的三角形是解题的关键.

练习册系列答案
相关题目
 如图,两个三角形图1和图2是否相似?说明你的理由.若相似,写出两组对应边的比例式.
如图,两个三角形图1和图2是否相似?说明你的理由.若相似,写出两组对应边的比例式.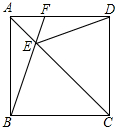 如图,在正方形ABCD中,AC为对角线,E为AC上一点,连接EB、ED.
如图,在正方形ABCD中,AC为对角线,E为AC上一点,连接EB、ED.