题目内容
11.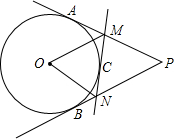 如图所示,已知PA、PB切⊙O于A、B两点,C是$\widehat{AB}$上一动点,过C作⊙O的切线交PA于点M,交PB于点N,已知∠P=56°,则∠MON=( )
如图所示,已知PA、PB切⊙O于A、B两点,C是$\widehat{AB}$上一动点,过C作⊙O的切线交PA于点M,交PB于点N,已知∠P=56°,则∠MON=( )| A. | 56° | B. | 60° | C. | 62° | D. | 不可求 |
分析 根据三角形内角和定理求出∠PMN+∠PNM的度数,根据补角的概念求出∠AMN+∠BNM,根据切线长定理得到∠CMO+∠CNO=$\frac{1}{2}$(∠AMN+∠BNM),根据三角形内角和定理计算即可.
解答 解:∠PMN+∠PNM=180°-∠P=124°,
∠AMN+∠BNM=360°-124°=236°,
∵MA、MC是⊙O的切线,
∴∠AMO=∠CMO,
∵NB、NC是⊙O的切线,
∴∠BNO=∠CNO,
∴∠CMO+∠CNO=$\frac{1}{2}$(∠AMN+∠BNM)=118°,
∴∠MON=180°-118°=62°,
故选:C.
点评 本题考查的是切线长定理的应用,切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.

练习册系列答案
相关题目
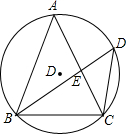 如图,AB=AC,弦BD⊥AC于点E.
如图,AB=AC,弦BD⊥AC于点E. 如图,在△ABC中,∠ABC=90°,CD⊥AB于点D,若AB=16,BC=12,求sinα.
如图,在△ABC中,∠ABC=90°,CD⊥AB于点D,若AB=16,BC=12,求sinα.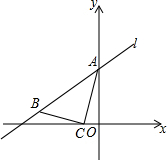 如图,直线l的表达式为y=kx+3(k>0),与y轴交于点A,点C在x轴的负半轴上,过点C作BC⊥AC交直线l于点B,且BC=CA,已知AC=$\sqrt{10}$,求k的值.
如图,直线l的表达式为y=kx+3(k>0),与y轴交于点A,点C在x轴的负半轴上,过点C作BC⊥AC交直线l于点B,且BC=CA,已知AC=$\sqrt{10}$,求k的值.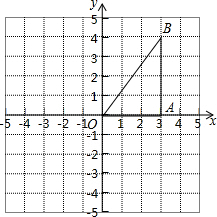 在10×10的网格纸上建立平面直角坐标系如图所示,在直角三角形ABO中,∠OAB=90°,且点B的坐标为(3,4).
在10×10的网格纸上建立平面直角坐标系如图所示,在直角三角形ABO中,∠OAB=90°,且点B的坐标为(3,4). 如图,E是线段AB中点,F是线段AE中点,已知图中所有线段的长度之和为52,求线段AE的长.
如图,E是线段AB中点,F是线段AE中点,已知图中所有线段的长度之和为52,求线段AE的长. 如图.AC,BD交于点O.图中共有8条线段,它们分别是CD,OC,OA,OD,OB,BD,AC,AB.
如图.AC,BD交于点O.图中共有8条线段,它们分别是CD,OC,OA,OD,OB,BD,AC,AB.