题目内容
6.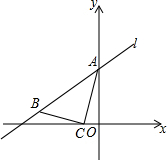 如图,直线l的表达式为y=kx+3(k>0),与y轴交于点A,点C在x轴的负半轴上,过点C作BC⊥AC交直线l于点B,且BC=CA,已知AC=$\sqrt{10}$,求k的值.
如图,直线l的表达式为y=kx+3(k>0),与y轴交于点A,点C在x轴的负半轴上,过点C作BC⊥AC交直线l于点B,且BC=CA,已知AC=$\sqrt{10}$,求k的值.
分析 作BD⊥x轴于D,根据题意求出OC的长,根据全等三角形的判定定理证明△BCD≌△CAO,求出点B的坐标,运用待定系数法解得即可.
解答  解:作BD⊥x轴于D,
解:作BD⊥x轴于D,
∵当x=0时,y=3,
∴点A的坐标为(0,3),即OA=3,
∵AC=$\sqrt{10}$,OA=3,
∴OC=$\sqrt{A{C}^{2}-O{A}^{2}}$=1,
∵BC⊥AC,
∴∠BCD+∠ACO=90°,又∠CAO+∠ACO=90°,
∴∠BCD=∠CAO,
在△BCD和△CAO中,
$\left\{\begin{array}{l}{∠BCD=∠CAO}\\{∠BDC=∠COA}\\{BC=CA}\end{array}\right.$,
∴△BCD≌△CAO,
∴BD=C0=1,CD=OA=3,
则OD=4,
∴点B的坐标为(-4,1),
则-4k+3=1,
解得k=$\frac{1}{2}$.
点评 本题考查的是一次函数知识的综合运用,掌握全等三角形的判定和性质、勾股定理、待定系数法求一次函数解析式是解题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
16.下列说法中正确的是( )
| A. | 1不是单项式 | B. | $\frac{x+y}{2}$是单项式 | C. | x2y的系数是0 | D. | $x-\frac{3}{2}$是整式 |
 把数字按如图所示排列起来,从上开始,依次为第一行、第二行、第三行.中间用虚线围的一列,从上至下:第一个数为1,第二个数为5,第三个数为13,第四个数为25,…,则第十个数为181,数“2015”在第六十三行,从左边数第2个.
把数字按如图所示排列起来,从上开始,依次为第一行、第二行、第三行.中间用虚线围的一列,从上至下:第一个数为1,第二个数为5,第三个数为13,第四个数为25,…,则第十个数为181,数“2015”在第六十三行,从左边数第2个.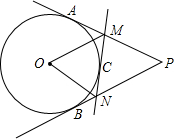 如图所示,已知PA、PB切⊙O于A、B两点,C是$\widehat{AB}$上一动点,过C作⊙O的切线交PA于点M,交PB于点N,已知∠P=56°,则∠MON=( )
如图所示,已知PA、PB切⊙O于A、B两点,C是$\widehat{AB}$上一动点,过C作⊙O的切线交PA于点M,交PB于点N,已知∠P=56°,则∠MON=( )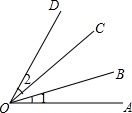 如图,若∠AOC=∠BOD,则∠1=∠2(填“>”、“<”或“=”).
如图,若∠AOC=∠BOD,则∠1=∠2(填“>”、“<”或“=”).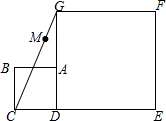 如图,四边形ABCD和四边形DEFG都是正方形.
如图,四边形ABCD和四边形DEFG都是正方形.