题目内容
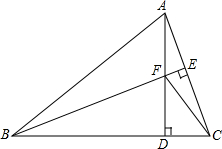 如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.(1)求证:△ADC≌△BDF;
(2)若CD=
| 2 |
考点:全等三角形的判定与性质,勾股定理
专题:
分析:(1)由AD⊥BC于点D,∠BAD=45°,就可以得出AD=BD,再由直角三角形的性质求出∠DAC=∠DBE就可以得出结论;
(2)由△ADC≌△BDF可以得出CD=ED,由勾股定理就可以求出CF,根据等腰三角形的性质就可以求出AE=CE,从而求出结论.
(2)由△ADC≌△BDF可以得出CD=ED,由勾股定理就可以求出CF,根据等腰三角形的性质就可以求出AE=CE,从而求出结论.
解答:解:(1)∵AD⊥BC,
∴∠ADB=∠ADC=90°.
∴∠ACD+∠DAC=90°.
∵∠BAD=45°,
∴∠ABD=45°,
∴∠BAD=∠DBA,
∴AD=BD.
∵BE⊥AC,
∴∠BEC=90°,
∴∠ACD+∠EBC=90°,∠ADB=∠ADC
∴∠DAC=∠DBF.
在△ADC和△BDF中,
,
∴△ADC≌△BDF(ASA);
(2)△ADC≌△BDF,
∴DC=DF.
∵CD=
,
∴DF=
.
在Rt△CDF中,由勾股定理,得
CF=2.
∵AB=BC,BE⊥AC,
∴AE=CE,
∴BE是AC的中垂线,
∴AF=CF,
∴AF=2,
∵AD=AF+DF,
∴AD=2+
.
答:AD的长为2+
.
∴∠ADB=∠ADC=90°.
∴∠ACD+∠DAC=90°.
∵∠BAD=45°,
∴∠ABD=45°,
∴∠BAD=∠DBA,
∴AD=BD.
∵BE⊥AC,
∴∠BEC=90°,
∴∠ACD+∠EBC=90°,∠ADB=∠ADC
∴∠DAC=∠DBF.

在△ADC和△BDF中,
|
∴△ADC≌△BDF(ASA);
(2)△ADC≌△BDF,
∴DC=DF.
∵CD=
| 2 |
∴DF=
| 2 |
在Rt△CDF中,由勾股定理,得
CF=2.
∵AB=BC,BE⊥AC,
∴AE=CE,
∴BE是AC的中垂线,
∴AF=CF,
∴AF=2,
∵AD=AF+DF,
∴AD=2+
| 2 |
答:AD的长为2+
| 2 |
点评:本题考查了等腰三角形的性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,中垂线的性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 我们分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0,则M<N.利用“作差法”解决下列问题:
我们分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0,则M<N.利用“作差法”解决下列问题: 甲、乙两地相距300千米,一辆轿车从甲地出发驶向乙地,同时一辆货车从乙地驶向甲地.如图,线段AB表示货车离甲地的距离y (千米)与行驶的时间x(小时)之间的函数关系;折线O-C-D表示轿车离甲地的距离y(千米)与行驶时间x(小时)之间的函数关系,请根据图象解答下列问题:
甲、乙两地相距300千米,一辆轿车从甲地出发驶向乙地,同时一辆货车从乙地驶向甲地.如图,线段AB表示货车离甲地的距离y (千米)与行驶的时间x(小时)之间的函数关系;折线O-C-D表示轿车离甲地的距离y(千米)与行驶时间x(小时)之间的函数关系,请根据图象解答下列问题: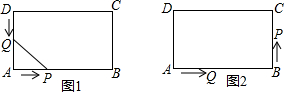 如图1,在长方形ABCD中,AB=12厘米,BC=6厘米.点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D开始向点A以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么:
如图1,在长方形ABCD中,AB=12厘米,BC=6厘米.点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D开始向点A以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么: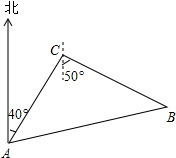 如图,某巡逻艇在A处发现北偏东40°相距9海里的C处有一艘走私船,正沿南偏东50°的方向以10海里/时的速度向我海岸行驶,巡逻艇立即以14海里/时的速度沿着直线方向追去,问需要多少时间才能追赶上该走私船?巡逻艇应该沿什么方向去追?
如图,某巡逻艇在A处发现北偏东40°相距9海里的C处有一艘走私船,正沿南偏东50°的方向以10海里/时的速度向我海岸行驶,巡逻艇立即以14海里/时的速度沿着直线方向追去,问需要多少时间才能追赶上该走私船?巡逻艇应该沿什么方向去追?
 “囧”(jiǒng)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
“囧”(jiǒng)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y. 如图,已知点E、C在线段BF上,BE=CF,请在下列四个等式中:①AB=DE,②∠ACB=∠F,③∠A=∠D,④AC=DF.选出两个作为条件,推出△ABC≌△DEF.并予以证明.(写出一种即可)
如图,已知点E、C在线段BF上,BE=CF,请在下列四个等式中:①AB=DE,②∠ACB=∠F,③∠A=∠D,④AC=DF.选出两个作为条件,推出△ABC≌△DEF.并予以证明.(写出一种即可) 将一副三角尺如图所示叠放在一起,则∠AEC的度数是
将一副三角尺如图所示叠放在一起,则∠AEC的度数是