题目内容
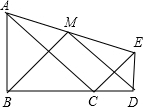 如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①AC2+CE2=AE2;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的个数是( )
如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①AC2+CE2=AE2;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的个数是( )| A、1个 | B、2个 | C、3个 | D、4个 |
考点:全等三角形的判定与性质,勾股定理
专题:
分析:②由三角形的面积公式、梯形的面积公式及不等式的基本性质a2+b2≥2ab(a=b时取等号)解答;
③过点M作MN⊥BD,垂足为N,则MN∥DE∥AB,根据平行线分线段成比例定理得出N为BD中点,由线段垂直平分线的性质得到BM=DM,再根据梯形中位线、等腰直角三角形的性质得出MN=
BD,则∠BMD=90°,判断③正确;
④通过作辅助线MN,构建直角梯形的中位线,根据梯形的中位线定理及等腰直角三角形的判定定理解答.
③过点M作MN⊥BD,垂足为N,则MN∥DE∥AB,根据平行线分线段成比例定理得出N为BD中点,由线段垂直平分线的性质得到BM=DM,再根据梯形中位线、等腰直角三角形的性质得出MN=
| 1 |
| 2 |
④通过作辅助线MN,构建直角梯形的中位线,根据梯形的中位线定理及等腰直角三角形的判定定理解答.
解答:解:如图,
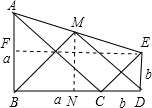
①作EF⊥AB,
则AF=a-b,EF=a+b,
∴AE2=AF2+EF2=(a+b)2+(a-b)2=2a2+2b2,
∵AC2=2a2,CE2=2b2,
∴AC2+CE2=AE2;故①正确;
②∵S△ABC=
a2,S△CDE=
b2,S梯形ABDE=
(a+b)2,
∴S△ACE=S梯形ABDE-S△ABC-S△CDE=ab,
S△ABC+S△CDE=
(a2+b2)≥ab(a=b时取等号),
∴S△ABC+S△CDE≥S△ACE;故②正确;
③过点M作MN垂直于BD,垂足为N.
∵点M是AE的中点,
则MN为梯形中位线,
∴MN=
(AB+ED)=
(BC+CD),
∴∠BMD=90°,即BM⊥DM;故③正确.
④过点M作MN垂直于BD,垂足为N.
∵点M是AE的中点,
则MN为梯形中位线,
∴N为中点,
∴△BMD为等腰三角形,
∴BM=DM;故④正确;
故选 D.

①作EF⊥AB,
则AF=a-b,EF=a+b,
∴AE2=AF2+EF2=(a+b)2+(a-b)2=2a2+2b2,
∵AC2=2a2,CE2=2b2,
∴AC2+CE2=AE2;故①正确;
②∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ACE=S梯形ABDE-S△ABC-S△CDE=ab,
S△ABC+S△CDE=
| 1 |
| 2 |
∴S△ABC+S△CDE≥S△ACE;故②正确;
③过点M作MN垂直于BD,垂足为N.
∵点M是AE的中点,
则MN为梯形中位线,
∴MN=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BMD=90°,即BM⊥DM;故③正确.
④过点M作MN垂直于BD,垂足为N.
∵点M是AE的中点,
则MN为梯形中位线,
∴N为中点,
∴△BMD为等腰三角形,
∴BM=DM;故④正确;
故选 D.
点评:本题考查了勾股定理的运用,考查了梯形中位线性质,考查了等腰三角形底边三线合一的性质.

练习册系列答案
相关题目
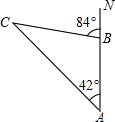 上午8时,一条船从海岛A出发,以15n mile/h(海里/时,1n mile=1852m)的速度向正北航行,10时到达海岛B处,从A、B望灯塔C,测得NAC=42°,NBC=84°.则从海岛B到灯塔C的距离为( )
上午8时,一条船从海岛A出发,以15n mile/h(海里/时,1n mile=1852m)的速度向正北航行,10时到达海岛B处,从A、B望灯塔C,测得NAC=42°,NBC=84°.则从海岛B到灯塔C的距离为( )| A、45n mile |
| B、30n mile |
| C、20n mile |
| D、15n mile |
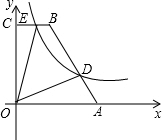 如图,在平面直角坐标系中,A(5,0)、B(2,6),BC∥AO,点D在AB上,BD=2AD,双曲线y=
如图,在平面直角坐标系中,A(5,0)、B(2,6),BC∥AO,点D在AB上,BD=2AD,双曲线y=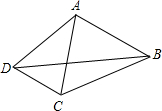 如图,在四边形ABCD中,CD∥AB,CB=4,AB=AC=AD=3,则BD的长为
如图,在四边形ABCD中,CD∥AB,CB=4,AB=AC=AD=3,则BD的长为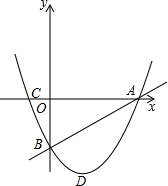 如图,抛物线y1=x2+bx-c经过直线y2=x-3与坐标轴的两个交点A、B,此抛物线与x轴的另一个交点为C,抛物线顶点为D.
如图,抛物线y1=x2+bx-c经过直线y2=x-3与坐标轴的两个交点A、B,此抛物线与x轴的另一个交点为C,抛物线顶点为D.