题目内容
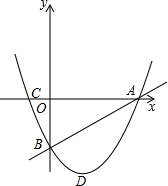 如图,抛物线y1=x2+bx-c经过直线y2=x-3与坐标轴的两个交点A、B,此抛物线与x轴的另一个交点为C,抛物线顶点为D.
如图,抛物线y1=x2+bx-c经过直线y2=x-3与坐标轴的两个交点A、B,此抛物线与x轴的另一个交点为C,抛物线顶点为D.(1)求此抛物线的解析式;
(2)求四边形ADBC的面积;
(3)直接写出使y1<y2的x的取值范围.
考点:二次函数的性质,一次函数的性质
专题:
分析:(1)对于一次函数y=x-3,分别令x与y为0求出对应y与x的值,确定出A与B的坐标,代入抛物线解析式得到关于b与c的方程组,求出方程组的解得到b与c的值,即可确定出抛物线解析式;
(2)分别求得A、B、C、D的坐标,利用S四边形ACBD=S△OBC+S梯形OBDE+S△AED求面积即可.
(3)根据y1<y2的可以得到抛物线位于直线的下方,从而可以写出自变量的取值范围.
(2)分别求得A、B、C、D的坐标,利用S四边形ACBD=S△OBC+S梯形OBDE+S△AED求面积即可.
(3)根据y1<y2的可以得到抛物线位于直线的下方,从而可以写出自变量的取值范围.
解答:解:(1)∵直线y=x-3与坐标轴的两个交点A、B,
∴点B(0,-3),点A(3,0),
将A与B坐标代入抛物线y=x2+bx-c得:
,
解得:c=3,b=-2,
则抛物线的解析式是y=x2-2x-3;
(2)∵令y=x2-2x-3=0,解得:x=-1或x=3,
∴点C的坐标为(-1,0),
∵y=x2-2x-3=(x-1)2+4,
∴顶点D的坐标为(1,-4),
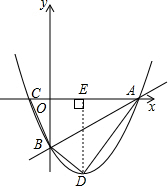
作DE⊥AC于点E,
由题意得:OC=1,OB=3,DE=4,OE=1,AE=2,
∴S四边形ACBD=S△OBC+S梯形OBDE+S△AED
=
OC•OB+
(OB+DE)•OE+
AE•ED
=
×1×3+
×(3+4)×1+
×2×4
=
+
+4
=9;
(3)∵y1<y2,
∴抛物线位于直线的下方,
∴x的取值范围为:0<x<3.
∴点B(0,-3),点A(3,0),
将A与B坐标代入抛物线y=x2+bx-c得:
|
解得:c=3,b=-2,
则抛物线的解析式是y=x2-2x-3;
(2)∵令y=x2-2x-3=0,解得:x=-1或x=3,
∴点C的坐标为(-1,0),
∵y=x2-2x-3=(x-1)2+4,
∴顶点D的坐标为(1,-4),

作DE⊥AC于点E,
由题意得:OC=1,OB=3,DE=4,OE=1,AE=2,
∴S四边形ACBD=S△OBC+S梯形OBDE+S△AED
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 3 |
| 2 |
| 7 |
| 2 |
=9;
(3)∵y1<y2,
∴抛物线位于直线的下方,
∴x的取值范围为:0<x<3.
点评:本题考查了二次函数的性质,解题的关键是能够求得图中的几个点的坐标,能够将点的坐标转化为线段的长,从而求得四边形的面积.

练习册系列答案
相关题目
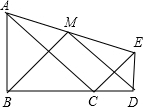 如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①AC2+CE2=AE2;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的个数是( )
如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①AC2+CE2=AE2;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的个数是( )| A、1个 | B、2个 | C、3个 | D、4个 |
下列四个算式中,正确的是( )
| A、(-5)+(+3)=-8 | ||
| B、-3+|-3|=0 | ||
C、(-1)÷5×
| ||
| D、-(-2)3=6 |
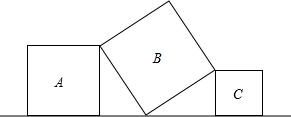 如图,将三个大小不同的正方形如图放置,顶点处两两相接,若正方形A的边长为4,C的边长为3,则B的边长为
如图,将三个大小不同的正方形如图放置,顶点处两两相接,若正方形A的边长为4,C的边长为3,则B的边长为