题目内容
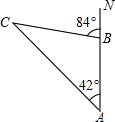 上午8时,一条船从海岛A出发,以15n mile/h(海里/时,1n mile=1852m)的速度向正北航行,10时到达海岛B处,从A、B望灯塔C,测得NAC=42°,NBC=84°.则从海岛B到灯塔C的距离为( )
上午8时,一条船从海岛A出发,以15n mile/h(海里/时,1n mile=1852m)的速度向正北航行,10时到达海岛B处,从A、B望灯塔C,测得NAC=42°,NBC=84°.则从海岛B到灯塔C的距离为( )| A、45n mile |
| B、30n mile |
| C、20n mile |
| D、15n mile |
考点:等腰三角形的判定与性质,方向角
专题:应用题
分析:根据三角形外角的性质,求证∠C=∠NAC,然后即可证明BC=AB,从而求得B到C的距离.
解答:解:∵∠NBC=84°,∠NAC=42°,
∴∠C=84°-42°=42°.
∴∠C=∠NAC,
∴BC=AB,
∵上午8时,一条船从海岛A出发,以150n mile/h的速度向正北航行.10时到达海岛B处,
∴BC=AB=15×2=30n mile.
故选B.
∴∠C=84°-42°=42°.
∴∠C=∠NAC,
∴BC=AB,
∵上午8时,一条船从海岛A出发,以150n mile/h的速度向正北航行.10时到达海岛B处,
∴BC=AB=15×2=30n mile.
故选B.
点评:此题考查了等腰三角形的判定和性质,灵活运用等腰三角形性质是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
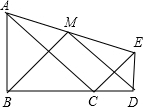 如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①AC2+CE2=AE2;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的个数是( )
如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①AC2+CE2=AE2;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的个数是( )| A、1个 | B、2个 | C、3个 | D、4个 |
估算
-3的值是( )
| 101 |
| A、在5与6之间 |
| B、在6与7之间 |
| C、在7与8之间 |
| D、在8与9之间 |
下列四个算式中,正确的是( )
| A、(-5)+(+3)=-8 | ||
| B、-3+|-3|=0 | ||
C、(-1)÷5×
| ||
| D、-(-2)3=6 |
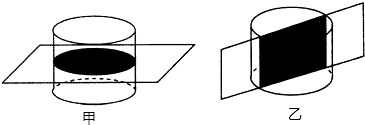 一个平面去截一个圆柱,图甲中截面的形状是
一个平面去截一个圆柱,图甲中截面的形状是