题目内容
14．多边形的对角线条数不可能是（ ）| A． | 2 | B． | 4 | C． | 9 | D． | 14 |
分析 根据对角线的关系式$\frac{1}{2}$n（n-3），即可得出n的值，再选择即可．
解答 解：当对角线为9时，可得出$\frac{1}{2}$n（n-3）=9，
解得n=$\frac{3±\sqrt{41}}{2}$（不合题意，舍去），
故选C．
点评 本题考查了多边形的对角线，熟记多边形对角线的关系式$\frac{1}{2}$n（n-3）是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
在-4，-3，-2，-1，1，2，3，4，m这9个数中，m代表一个数，你认为m是多少时，能够使这9个数分别填入图中的9个空格内，使每行的3个数、每列3个数、斜对角3个数个数相加均为零．
5．下列方程中，是关于x的一元二次方程的是（ ）
| A． | 3（x+1）2=2（x+1） | B． | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 | C． | ax2+bx+c=0 | D． | 2x+1=0 |
2．下列说法正确的是（ ）
| A． | 有理数包括正整数、零和负分数 | |
| B． | -a不一定是整数 | |
| C． | -5和+（-5）互为相反数 | |
| D． | 两个有理数的和一定大于每一个加数 |
19．
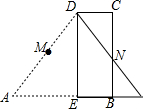如图，设M，N分别是直角梯形ABCD两腰的中点，DE⊥AB，将△ADE沿DE翻折，M、N恰好重合，则AB：BE等于（ ）
如图，设M，N分别是直角梯形ABCD两腰的中点，DE⊥AB，将△ADE沿DE翻折，M、N恰好重合，则AB：BE等于（ ）| A． | 2：1 | B． | 1：2 | C． | 3：1 | D． | 1：3 |
某自行车厂生产产量如下图表所示，5月份产量比4月份减少了10%，且6、7月份增长率均为x，求增长的百分率．
如图，O为AB上一点，将该图形沿OG对折后两侧能完全重合，若∠B=25°，∠DOC=90°，求∠AED的度数．
如图，在△ABC中，AB=10，AC=8，O为△ABC角平分线的交点，若△ABO的面积为20，则△ACO的面积为16．