如图.设M.N分别是直角梯形ABCD两腰的中点.DE⊥AB.将△ADE沿DE翻折.M.N恰好重合.则AB:BE等于( )A．2:1B．1:2C．3:1D．1:3 题目和参考答案——青夏教育精英家教网——

题目内容

19．

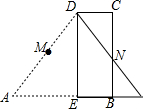如图，设M，N分别是直角梯形ABCD两腰的中点，DE⊥AB，将△ADE沿DE翻折，M、N恰好重合，则AB：BE等于（　　）

A．

2：1

B．

1：2

C．

3：1

D．

1：3

分析先设DE与MN交于点F，由于MN是AD、BC的中点，所以根据梯形中位线定理，可知MN∥AB，在△ADE中，MF∥AE，M是AD中点，根据平行线分线段成比例定理，可知F也是DE中点，利用三角形中位线定理，可知AE=2MF，又由于△ADE沿DE翻折，MN重合，可知MF=NF，在根据四边形FEBN是矩形，可知NF=BE，那么就可求出AB：BE的值

解答解：设DE与MN交于点F，
∵M、N分别是AD、CB上的中点，
∴MN∥AB，
又∵M是AD的中点，
∴MF=$\frac{1}{2}$AE，
又∵M、N重合，
∴NF=BE，MF=NF，
∴AB：BE=2MF：NF=3：1，
故选：C．

点评本题考查的是翻折变换的性质，翻折变换是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．

练习册系列答案

追击小考小学毕业升学总复习系列答案

一线名师云南密卷系列答案

化学教与学系列答案

四川新教材新中考系列答案

系统分类总复习系列答案

新课标阶梯阅读训练系列答案

考前模拟预测试卷系列答案

同步词汇训练系列答案

优加学案创新金卷系列答案

单元自测系列答案

相关题目

9．小丽是个爱思考的学生，最近，她发现一些特殊的两位数乘法，如：
21×29=609；23×27=621；31×39=1209；52×58=3016；…
其因数和计算结果都存在一定的规律
请你观察上述算式，寻找它们的特征和规律，回答下列问题．
（1）下列算式中，与上述算式具有同样特征的是B
A、23×24=552，B、34×36=1224；
（2）试写出一个与上述算式具有同样特征的算式：32×38=1216；
（3）为了反映上述规律，如果设其中一个因数十位上的数字为a，个位数字为b，那么该因数可表示为10a+b，另一个因数可表示为10a+10-b，计算结果可表示为100a（a+1）+b（10-b），从而上述算式的特征和规律可用一个等式表示为（10a+b）（10a+10-b）=100a（a+1）+b（10-b）．
（4）试运用你所学的知识说明（3）中写出的等式是正确的．

如图，∠MON=30°，点A₁、A₂、A₃…在射线ON上，点B₁、B₂、B₃…在射线OM上，△A₁B₁A₂、△A₂B₂A₃、△A₃B₃A₄…均为等边三角形，依此类推，若OA₁=1，则△A₂₀₁₆B₂₀₁₆A₂₀₁₇的边长为（　　）

2²⁰¹⁶

2²⁰¹⁵

7．若a是方程x²-x-2=0的一个根，求（a²-a）（a-$\frac{1}{a}$+1）的值．

14．多边形的对角线条数不可能是（　　）

4．分别写出下列各数的平方根和算术平方根：
（1）2$\frac{1}{4}$；（2）$\sqrt{16}$；（3）（-4）²．

7．m何值时x²+mx+3=0与x²-4x-（m-1）=0有一个公共解？并求出该公共解．

如图，直角△ABC中，AB=5，BC=3，AC=4，直角△ABC将沿着它的一条边AB旋转一周，得到一个什么图形？试求出其表面积和点C运动的路程．

5．已知二次函数y=（x+1）²+2，当x＞-1时，y随x的增大而增大．