题目内容
4. 在-4,-3,-2,-1,1,2,3,4,m这9个数中,m代表一个数,你认为m是多少时,能够使这9个数分别填入图中的9个空格内,使每行的3个数、每列3个数、斜对角3个数个数相加均为零.
在-4,-3,-2,-1,1,2,3,4,m这9个数中,m代表一个数,你认为m是多少时,能够使这9个数分别填入图中的9个空格内,使每行的3个数、每列3个数、斜对角3个数个数相加均为零.(1)我认为m=0.
(2)按要求将这9个数填入如图的空格内.
(3)在这9个数中任选四个数,利用有理数的混合运算,使四个数的运算结果为24(注意:每个数只能用一次).
分析 (1)根据题意可以推测数m的值;
(2)根据题意可以把表格补充完整;
(3)根据题意可以写出符合要求的式子,只要写出一个即可.
解答  解:(1)由题意可得,
解:(1)由题意可得,
m的值为0,
故答案为:0;
(2)如右图所示,
(3)由题意可得,
4×(1+2+3)=24.
点评 本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
14.实数-$\sqrt{27}$,0,($\sqrt{2}$)0,$\root{3}{125}$,0.7070070007…(相邻两个7之间0的个数逐次增加),3.$\stackrel{•}{2}\stackrel{•}{5}$,$\sqrt{(-5)^2}$,2π中,无理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
15.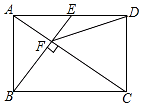 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列四个结论:
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列四个结论:
①△AEF∽△CAB; ②CF=2AF; ③DF=DC; ④S四边形CDEF=$\frac{5}{2}$S△AEF,
其中正确的结论有( )个.
 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列四个结论:
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列四个结论:①△AEF∽△CAB; ②CF=2AF; ③DF=DC; ④S四边形CDEF=$\frac{5}{2}$S△AEF,
其中正确的结论有( )个.
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
12.下列各数中互为相反数的是( )
| A. | -$\frac{1}{2}$与0.2 | B. | $\frac{1}{3}$与-0.33 | C. | -2.25与2$\frac{1}{4}$ | D. | 5与-(-5) |
14.多边形的对角线条数不可能是( )
| A. | 2 | B. | 4 | C. | 9 | D. | 14 |
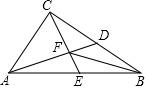 如图,在Rt△ABC中,∠ACB=90°,AD、CE分别是BC、AB边上的中线,且满足AD⊥CE,垂足为F,联结BF.
如图,在Rt△ABC中,∠ACB=90°,AD、CE分别是BC、AB边上的中线,且满足AD⊥CE,垂足为F,联结BF.