题目内容
已知关于x的方程(k+1)x2+2x-1=0有实根,求k的最小整数值.
考点:根的判别式,一元一次方程的解,一元二次方程的定义
专题:
分析:分该方程为一元一次方程和一元二次方程来讨论,得出关于k的等式或不等式求出k的最小整数值即可.
解答:解:当方程为一元一次方程时,k+1=0,此时方程为2x-1=0有解,此时k=-1,
当方程为一元二次方程时,k+1≠0,且判别式△≥0,
即4+4(k+1)≥0,
解得k≥-2且k≠-1,
综上可知k的取值范围为k≥-2,
所以其最小整数值为-2.
当方程为一元二次方程时,k+1≠0,且判别式△≥0,
即4+4(k+1)≥0,
解得k≥-2且k≠-1,
综上可知k的取值范围为k≥-2,
所以其最小整数值为-2.
点评:本题主要考查根的判别式的应用,分两种情况讨论求出k的取值范围是解题的关键.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,点A(
如图,在平面直角坐标系xOy中,点A(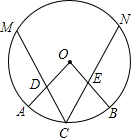 如图,在⊙O中,点C为
如图,在⊙O中,点C为
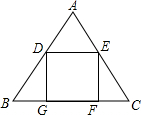 如图,等边三角形ABC中,G、F是BC边上两点,点D、E分别在边AB和AG上,四边形DGFE是长方形,若BG=1,AD=3,则BC=
如图,等边三角形ABC中,G、F是BC边上两点,点D、E分别在边AB和AG上,四边形DGFE是长方形,若BG=1,AD=3,则BC=