题目内容
17.张三同学投掷一枚骰子两次,两次所投掷的点数分别用字母m、n表示(1)求使关于x的方程x2-mx+2n=0有实数根的概率;
(2)求使关于x的方程mx2+nx+1=0有两个相等实根的概率.
分析 (1)画树状图展示所有36种等可能的结果数,然后根据判别式的意义找出满足△=m2-8n≥0的结果数,然后根据概率公式求解;
(2)根据判别式的意义找出满足△=n2-4m=0的结果数,然后根据概率公式求解.
解答 解:(1)画树状图为:
共有36种等可能的结果数,其中满足△=m2-8n≥0的结果数为10,
所以使关于x的方程x2-mx+2n=0有实数根的概率=$\frac{10}{36}$=$\frac{5}{18}$;
(2)满足△=n2-4m=0的结果数为2,
所以使关于x的方程mx2+nx+1=0有两个相等实根的概率=$\frac{2}{36}$=$\frac{1}{18}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了判别式的意义.

练习册系列答案
相关题目
7.我市5月的某一周每天的最高气温(单位:℃)统计如下:19,20,25,22,25,26,27,则这组数据的中位数与众数分别是( )
| A. | 25,25 | B. | 25,22 | C. | 20,22 | D. | 22,24 |
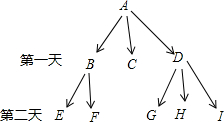 A同学心里有一个秘密,这个秘密按图中箭头指向在A,B,C,D,E,F,G,H,I这9个同学中传播,将这个秘密告诉过B的同学或者B将这个秘密告诉过的同学都不会再告诉B这个秘密.(注:不同的字母代表不同的同学)
A同学心里有一个秘密,这个秘密按图中箭头指向在A,B,C,D,E,F,G,H,I这9个同学中传播,将这个秘密告诉过B的同学或者B将这个秘密告诉过的同学都不会再告诉B这个秘密.(注:不同的字母代表不同的同学)
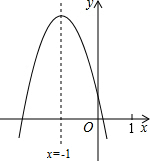 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2-4ac<0;②4a+c>2b;③3b+2c<0;④4n(an+b)≤a,其中结论正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2-4ac<0;②4a+c>2b;③3b+2c<0;④4n(an+b)≤a,其中结论正确的个数是( )