题目内容

5．先化简，再求值：（$\frac{x+2}{{x}^{2}-2x}$-$\frac{x-1}{{x}^{2}-4x+4}$）÷$\frac{{x}^{2}-16}{{x}^{2}+4x}$，并选一个你喜欢的x的值代入求值．

分析 先根据分式混合运算的法则把原式进行化简，再选取合适的x的值代入进行计算即可．

解答 解：原式=[$\frac{x+2}{x（x-2）}$-$\frac{x-1}{（x-2）^{2}}$]•$\frac{x（x+4）}{（x+4）（x-4）}$
=$\frac{{x}^{2}-4-{x}^{2}+x}{x{（x-2）}^{2}}$•$\frac{x}{x-4}$
=$\frac{x-4}{x{（x-2）}^{2}}$•$\frac{x}{x-4}$
=$\frac{1}{{（x-2）}^{2}}$，
当x=1时，原式=$\frac{1}{{（1-2）}^{2}}$=1．

点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．

练习册系列答案
相关题目
15．两圆的半径分别为5和6，当两圆相交时，圆心距d的取值范围为1＜d＜11．
16．下列计算正确的是（　　）
A．$\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$B．$\sqrt{12}$÷$\sqrt{3}$=2C．$\sqrt{6}$×（-$\sqrt{3}$）=3$\sqrt{2}$D．（$\sqrt{3}$-1）2=2
13．在平面直角坐标系中，点P（2，-1）关于原点O的对称点在（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
20．下列关系式中，正确的是（　　）
A．（a+b）2=a2-2ab+b2B．（a-b）2=a2-b2C．（a+b）2=a2+b2D．（a+b）（a-b）=a2-b2
10．已知直线a，b被直线c，d所截，a∥b，且直线c⊥直线a，直线d⊥直线b，则直线c与直线d之间的位置关系是平行．（填“平行”“相交”或“垂直”）
17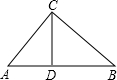．如图，在Rt△ABC中，∠ACB=90°，AB=$\sqrt{13}$，BC=2，则这个直角三角形的面积为（　　）
A．3B．6C．$\sqrt{13}$D．$\frac{1}{2}$$\sqrt{13}$
14．下列各式中，有意义的是（　　）
A．$\sqrt{\frac{1}{9}-1}$B．$\sqrt{-2}$C．$-\sqrt{{{（{-6}）}^3}}$D．$\sqrt{{{（{-3}）}^2}}$
15．$\sqrt{16}$=（　　）
A．±2B．2C．±4D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网