题目内容
17．
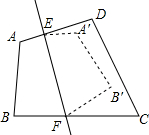如图，四边形ABCD沿直线EF对着，点A、B的对应点A′，B′落在四边形内部，若∠C+∠D=160°，则∠DEA′+∠CFB′的度数是40°．
分析 在四边形ABCD中可知：∠A+∠B=200°，由翻折的性质可知：∠A′+∠B′=200°，在四边形EA′B′F中，∠A′EF+∠B′FE=160°，在四边形DEFC中，∠DEF+∠EFC=200°，根据∠DEA′+∠CFB′=∠DEF+∠EFC-（∠A′EF+∠B′FE）即可求得答案．
解答 解：在四边形ABCD中，∠C+∠D=160°，
∴∠A+∠B=200°，
由翻折的性质可知：∠A′+∠B′=200°，
在四边形EA′B′F中，∠A′EF+∠B′FE=360°-200°=160°，
在四边形DEFC中，∠DEF+∠EFC=360°-160°=200°，
∴∠DEA′+∠CFB′=∠DEF+∠EFC-（∠A′EF+∠B′FE）=200°-160°=40°．
故答案为：40°．
点评 本题主要考查的是翻折变换和四边形的内角和，利用翻折的性质以及任意四边形的内角和是360°进行角的转化与计算是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
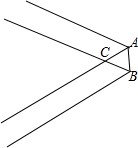如图，若将宽为3cm的矩形纸片沿AB折叠成∠ACB=45°，那么△ABC的面积为$\frac{9\sqrt{2}}{2}$cm2．
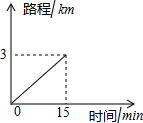小丽家离学校2km，步行到校需30min，小丽的同学小军上学要经过小丽家，小军骑车上学行驶的路程与时间的关系如图所示． 
如图，矩形ABCD中，AB=4，BC=3，动点E从B点出发，沿B-C-D-A运动至A点停止，设运动的路程为x，△ABE的面积为y，则y与x的函数关系用图象表示正确的是（ ）
