题目内容
7.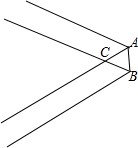 如图,若将宽为3cm的矩形纸片沿AB折叠成∠ACB=45°,那么△ABC的面积为$\frac{9\sqrt{2}}{2}$cm2.
如图,若将宽为3cm的矩形纸片沿AB折叠成∠ACB=45°,那么△ABC的面积为$\frac{9\sqrt{2}}{2}$cm2.
分析 易证∠1=∠2=∠CAB,可得出AC=BC,过A作AD⊥BC,垂足为D,在Rt△ACD中,先求出AC的长,继而求出BC的长,根据面积公式计算即可.
解答 解:∵MA∥NB,
∴∠1=∠2,
∵∠1=∠CAB,
∴∠2=∠CAB,
∴AC=BC,
如图,过A作AD⊥BC,垂足为D,
∵∠ACB=45°,AD⊥BC,AD=3cm,
∴AC=3$\sqrt{2}$cm,
∵AC=BC,
∴BC=3$\sqrt{2}$cm,
∴S△ABC=$\frac{1}{2}$×3$\sqrt{2}$×3=$\frac{9\sqrt{2}}{2}$cm2.
故答案为:$\frac{9\sqrt{2}}{2}$cm2.
点评 本题考查了翻折变换的问题,综合性较强,注意熟练掌握翻折不变性、平行线的性质、等腰三角形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
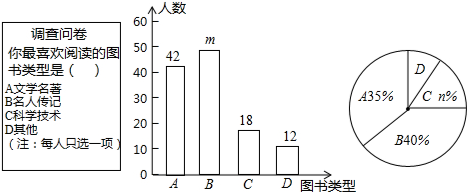
 如图,?DEFG内接于△ABC,已知△ADE、△EFC、△DBG的面积分别为1,2.8和1.2,则?DEFG的面积是4.
如图,?DEFG内接于△ABC,已知△ADE、△EFC、△DBG的面积分别为1,2.8和1.2,则?DEFG的面积是4. 如图,已知BE是△ABC的外接圆的直径,CD⊥AB于D,若AD=3,BD=8,CD=6,则BE的长为5$\sqrt{5}$.
如图,已知BE是△ABC的外接圆的直径,CD⊥AB于D,若AD=3,BD=8,CD=6,则BE的长为5$\sqrt{5}$.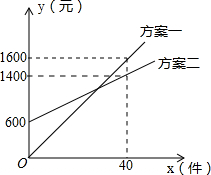 某销售公司推销一种产品,设x(种)是推销产品的数量,y(元)是付给推销员的月报酬.公司付给推销员的月报酬的两种方案如图所示,推销员可以任选一种与公司签订合同,看图解答下列问题:
某销售公司推销一种产品,设x(种)是推销产品的数量,y(元)是付给推销员的月报酬.公司付给推销员的月报酬的两种方案如图所示,推销员可以任选一种与公司签订合同,看图解答下列问题: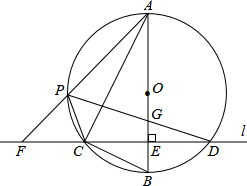 如图,在⊙O的内接△ABC中,∠ACB=90°,tan∠CAB=$\frac{1}{2}$,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是$\widehat{AC}$上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
如图,在⊙O的内接△ABC中,∠ACB=90°,tan∠CAB=$\frac{1}{2}$,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是$\widehat{AC}$上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.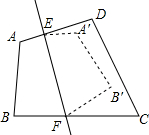 如图,四边形ABCD沿直线EF对着,点A、B的对应点A′,B′落在四边形内部,若∠C+∠D=160°,则∠DEA′+∠CFB′的度数是40°.
如图,四边形ABCD沿直线EF对着,点A、B的对应点A′,B′落在四边形内部,若∠C+∠D=160°,则∠DEA′+∠CFB′的度数是40°.